Consider two straight lines, each of which is tangent to both the circle x2+y2=12 and the parabola y2=4x . Let these lines intersect at the point Q . Consider the ellipse whose center is at the origin O(0, 0) and whose semi-major axis is OQ . If the length of the minor axis of this ellipse is √2 , then which of the following statement(s) is (are) TRUE? Solution in Bengali
For the ellipse, the eccentricity is 1√2 and the length the latcus rectum is 1
For the ellipse, the eccentricity is 12 and the length the latcus rectue is 12
The area of the reagion bounded by the ellipse between the lines x=1√2andx=1is14√4(π−2)
The area of the region bounded by the ellipse between the lines x=1√2andx=1is116(π−12)
The correct Answer is:A:C
Equation of tangent of parabola y2=4x having slop is y=mx+1m ltbr If this is tangent to circle x2+y2=1/2.
If this is tangent of circle x2+y2=1/2, then distance form centre of the circle from the line is equal to radius.
∴∣∣
∣∣0+0+1m√1+m2∣∣
∣∣=1√2
∴m4+m2−2=0
∴m=±
Euqation of common tangens are y=x+1andy=−x−1
These tangents intersects at point Q which is (-1,0) .
∴OQ=1
Let the equation of ellipese be x2a2+y2b2=1
∴a=OQ=1
Let the equation of ellipse be x2a2+y2b2=1
∴a=OQ=1
also, given that 2b=√2orb=1√2
Thererfore, equation of ellipse is x21+y21/2=1
e=√1−b2a2=√1−12=1√2
L.R.=2b2a=1
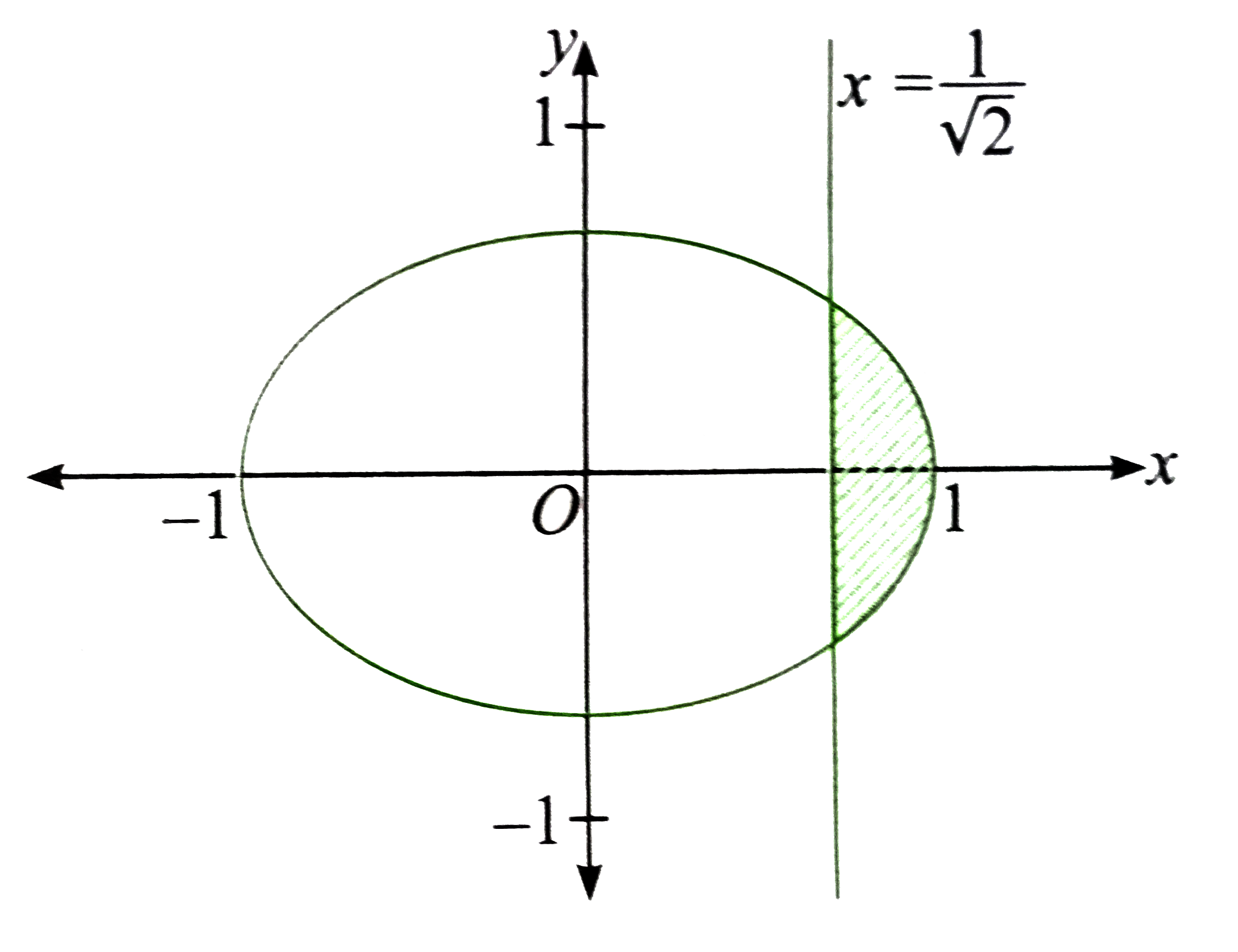
Leh the area bounded by ellipse and lines x=1√2andx=1 be A.
A=2×1∫1/√21√2√1−x2dx
=√2[x2√1−x2+12sin−1x]11/√2
=√2[π4−(14+π8)]=√2(π8−14)=π−24√2
Similar Questions
Statement 1 : The equations of the tangents drawn at the ends of the major axis of the ellipse 9x2+5y2−30y=0 is y=0,y=6 . Statement 2 : The tangents drawn at the ends of the major axis of the ellipse x2a2+y2b2=1 are always parallel to the y-axis.
View Solutionमाना वृत्त x2+y2=9 तथा परवलय y2=8x है। यह प्रथम तथा चतुर्थ चतुर्थाश में क्रमशः P तथा Q पर प्रतिच्छेद करते है। वृत्त की P तथा Q पर स्पर्श रेखाएं x-अक्ष को R पर प्रतिच्छेद करती है तथा परवलय की P तथा Q पर स्पर्श रेखा x-अक्ष को S पर प्रतिच्छेद करती है।
त्रिभुज PRS के परिवृत्त की त्रिज्या है-
View Solutionमाना वृत्त x2+y2=9 तथा परवलय y2=8x है। यह प्रथम तथा चतुर्थ चतुर्थाश में क्रमशः P तथा Q पर प्रतिच्छेद करते है। वृत्त की P तथा Q पर स्पर्श रेखाएं x-अक्ष को R पर प्रतिच्छेद करती है तथा परवलय की P तथा Q पर स्पर्श रेखा x-अक्ष को S पर प्रतिच्छेद करती है।
त्रिभुज PQR के अन्तःवृत्त की त्रिज्या है-
View Solutionऐसी दो सरल रेखाओं पर विचार कीजिए, जिनमें से प्रत्येक वृत्त x2+y2=12 और परवलय y2=4x दोनों पर ही स्पर्शी है | माना कि ये रेखाएं बिन्दु Q पर प्रतिछेद करती है | एक ऐसी दीर्घवृत्त पर विचार कीजिये जिसका केन्द्र मूलबिंदु O(0,0) पर है और जिसका अर्ध - दीर्घ अक्ष O Q है | यदि इस दीर्घवृत्त के लघु अक्ष की लम्बाई √2 है, तब निम्नलिखित में से कौन सा (से) कथन सत्य है (हैं)
View Solutionमाना वृत्त x2+y2=9 तथा परवलय y2=8x है | वे P तथा Q पर क्रमश: प्रथम तथा चतुर्थ चतुर्थांश में प्रतिच्छेद करते हैं | P तथा Q पर वृत्त की स्पर्श रेखाऐं x-अक्ष को R पर प्रतिच्छेद करती हैं तथा P व Q पर परवलय की स्पर्श रेखाऐं x-अक्ष को S पर प्रतिच्छेद करती हैं |
ΔPQS तथा ΔPQR के क्षेत्रफल का अनुपात है
View SolutionThe poisson's ratio for O2 is 1.4. Which of the following are correct for O2?
View SolutionIf (0,3+√5) is a point on the ellipse whose foci and (2, 3) and (−2,3), then the length of the semi - major axis is
View SolutionStatement 1 : The equations of the tangents drawn at the ends of the major axis of the ellipse 9x^2+5y^2-30 y=0 is y=0,y=6 . Statement 2 : The tangents drawn at the ends of the major axis of the ellipse (x^2)/(a^2)+(y^2)/(b^2)=1 are always parallel to the y-axis.
View Solution
