Two sets A and B are as under A=|(a,b)∈R×R|a−5|<1and|b−5∣<1}B=[(a,b)∈R×R:4(a−6)2+9(b−5)2≤36}Then: (1) B⊂A (2) A⊂B (3) A∩B=ϕ(anemptyset)(4)≠itherA sub BnorB sub ASolution in Bengali
neither A⊂BnorB⊂A
B⊂A
A⊂B
A⊂B=ϕ (an empty set)
Let a x=a and b=y
So, we have |x−5|<1and|y−5|<1 (1)
|x−5|<1
⇒−1<x−5<1
⇒4<x<6
Similary, 4<yl,t6
Thus, we have a square for inequality (1)
Now,4(x−6)2+9(y−5)2≤36
⇒(x−6)29+(y−5)24≤ (2)
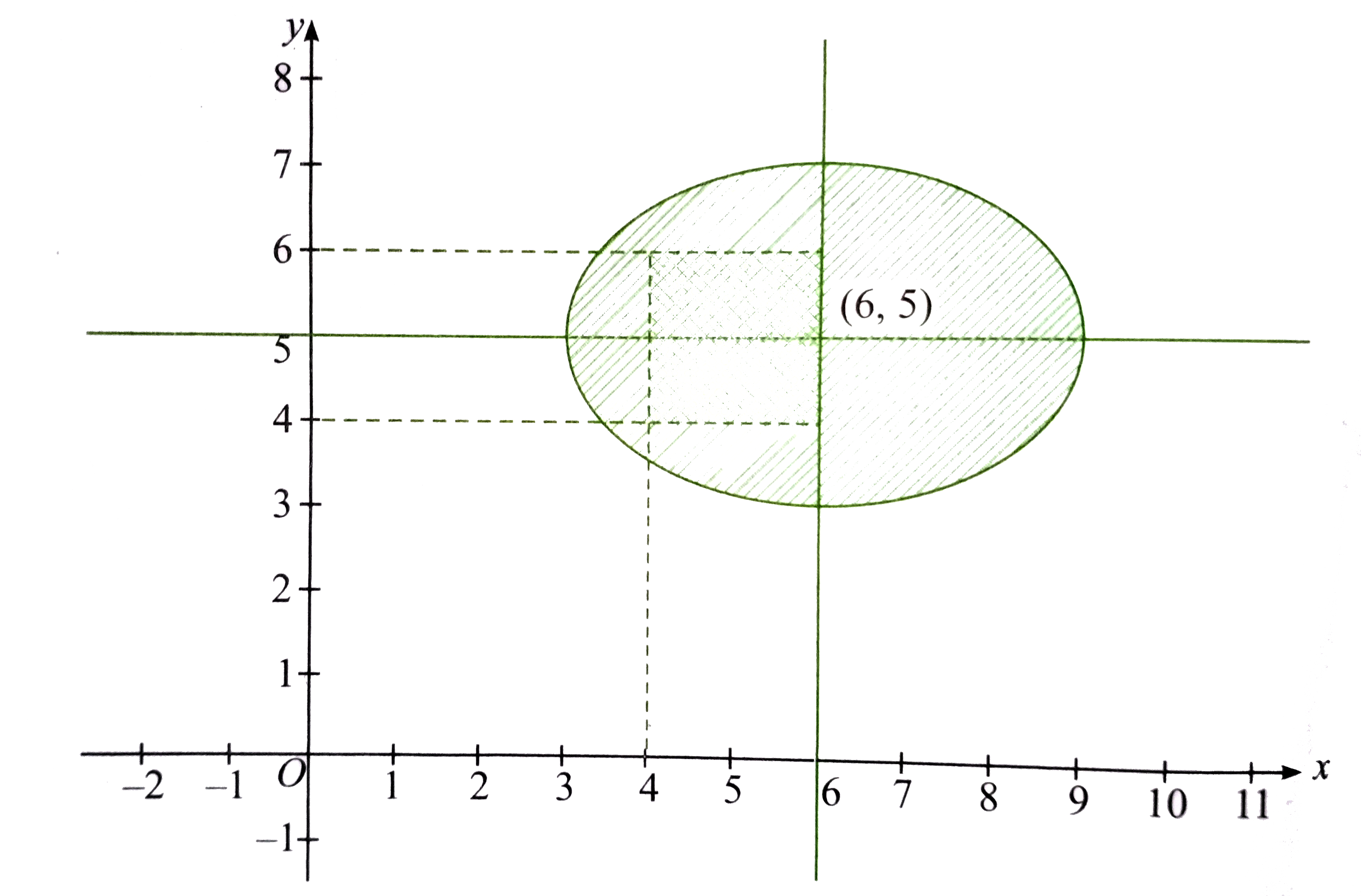
Points satsfying above indquality lies inside ellipse or on the ellipse having center at (6,5).
Regios of both the inequalities are plotted as shown in the following figure :
Similar Questions
The sets A and B are following, A={(a,b)∈R×R:[a−5]<1 and |b−5|<1},B={(a,b)∈R×R:4(a−6)2+9(b−5)2≤36}. Then
View Solutionदो समुच्चय A तथा B निम्न प्रकार के हैं
A={(a,b)∈R×R:|a−5| तथा |b−5|<1} ,
B={(a,b)∈R×R:4(a−6)2+9(b−5)2≤36} ,
तो : (i) A∩B=ϕ (ii) न तो A⊂B और न ही B⊂A (iii) B⊂A (iv) A⊂B
View SolutionTwo sets A and B are as under A=|(a,b) in RxxR:|a-5| lt 1 and |b-5| lt 1} B=[(a,b) in Rxx R:4(a-6)^2+9(b-5)^2 le 36} Then: (1) B sub A (2) A sub B (3) AnnB =phi ( an empty set) (4) neither A sub B nor B sub A
View SolutionDetermine if A sub B or A cancel sub B where A=ϕ,B={ϕ}
View SolutionTwo sets A and B are as under A=|(a,b) in RxxR:|a-5| lt 1 and |b-5| lt 1} B=[(a,b) in Rxx R:4(a-6)^2+9(b-5)^2 le 36} Then: (1) B sub A (2) A sub B (3) AnnB =phi ( an empty set) (4) neither A sub B nor B sub A
View SolutionA⊂B ଓ B⊂A ହେଲେ A ଓ B ସେଟ ମଧ୍ୟରେ କଣ ସଂମ୍ପର୍କ ଲେଖ |
View SolutionConsider the following set : phi, A= {1, 3}, B = {1, 5, 9},C= {1, 3, 5, 7, 9}. Insert the correct symbol sub or cancel (sub) between pair of sets : phi .............. B .
View SolutionConsider the following set : phi, A= {1, 3}, B = {1, 5, 9},C= {1, 3, 5, 7, 9} . Insert the correct symbol sub or cancel (sub) between pair of sets : A.........B.
View Solution
