A point moves so that the sum of the squares of its distances from two intersecting straight lines is constant. Prove that its locus is an ellipse.Solution in Bengali
√cos2αsinαifα<π4
√−cos2αcosαifα<π4
√cos2αcosαifα<π4
√−cos2αsinαifα<π4
Let us chosse the point of intersection of the givne lines as the origin and their angular bisector as the x-axis. Thenequation of the two lines will bey mx and y=-mx , where = tanα,
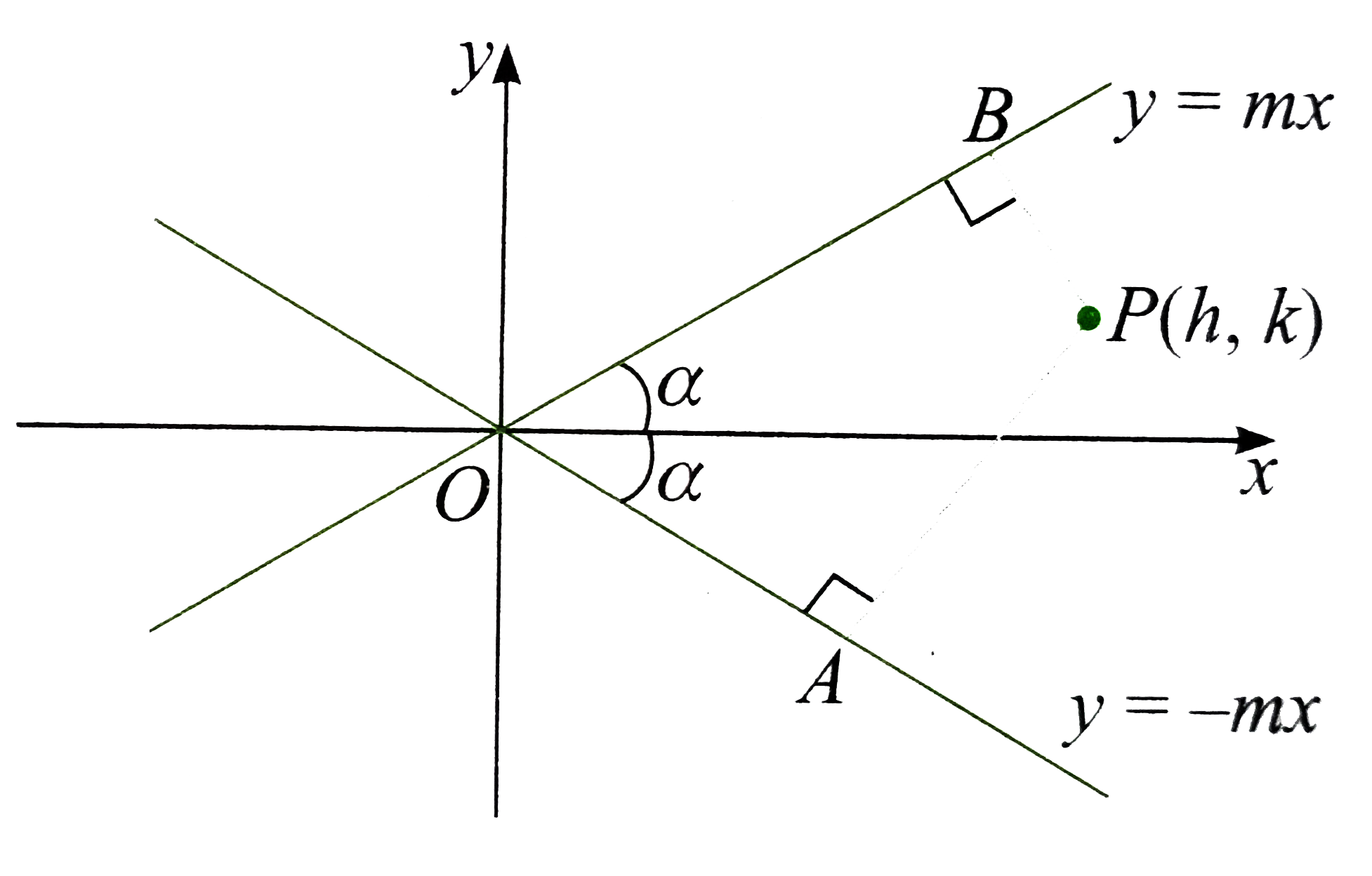
Let P(h,k) be the point whose locus is to be foud.
Then accroding toe the given condition,
PA2+PB2= Constant
⇒(k−mh)21+m2+(k+mh)21+m2 (c is constant)
⇒2(k2+m2h2)=c(1+m2)
Therfore, the locus of pointP is
x2a2+y2b2=1
where a2=c(1+m2)2m2andb2=c(1+m2)2 M
If α<π/4, then m<1,anda2>b2
∴ Ecentricity =√1−b2a2=√1−m2=√cos2αcosα
If α>π/4 then m>1anda2<b2
∴ Ecentricity =√1−b2a2=√1−1m2=√−cos2αsinα
Similar Questions
Prove that the locus of the point that moves such that the sum of the squares of its distances from the three vertices of a triangle is constant is a circle.
04:21View SolutionThe locus of a point which moves such that the sum of the square of its distance from three vertices of a triangle is constant is a/an circle (b) straight line (c) ellipse (d) none of these
04:27View SolutionA point moves so that the sum of the squares of its distances from two intersecting straight lines is constant. Prove that its locus is an ellipse.
04:37View SolutionA point moves so that the sum of squares of its distances from the points (1, 2) and (−2,1) is always 6. Then its locus is
06:09View Solutionएक बिन्दु का बिन्दुपथ ज्ञात कीजिए, जो इस प्रकार गतिमान है कि दो प्रतिच्छेदी रेखाओं से इसकी दूरियों का योगफल सदैव नियत है।
03:01View SolutionThe locus of a point which moves so that the difference of the squares of its distance from two given points is constant, is a
04:08View SolutionThe locus of a point which moves such that the sum of the square of its distance from three vertices of a triangle is constant is a/an (a)circle (b) straight line (c) ellipse (d) none of these
04:35View SolutionProve that the locus of the point that moves such that the sum of the squares of its distances from the three vertices of a triangle is constant is a circle.
02:37View Solution
