about to only mathematics Solution in Bengali

A

9

B

13

C

4

D

5

Video Solution

Text Solution

Verified by Experts

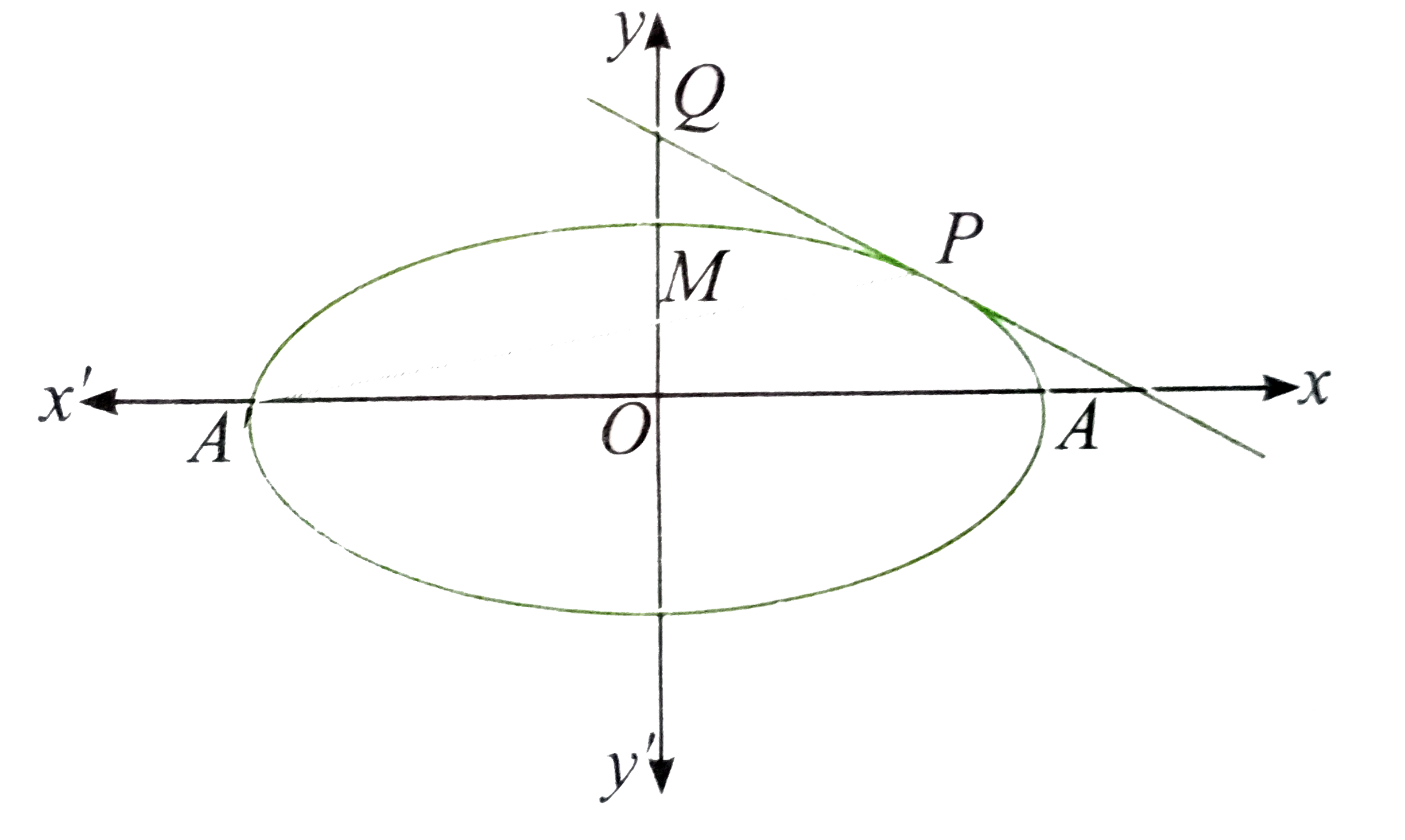
Let the P be $(a cos θ b, sin θ)$
The equation of the tangent at point P is $\frac{x}{a} cos θ + \frac{y}{b} sin θ = 1$
The point Q is $(0, b s cosec θ)$
The quation of chord A'P is
$y - 0 = \frac{b sin θ}{a cos θ + a} (x + a)$
Putting x=0, we have
$y = \frac{b sin θ}{cos t h e a + 1}$
Then,
$O Q^{2} - M Q^{2} = b^{2} {coses}^{2} θ - {(b cosec θ - \frac{b sin θ}{cos θ + 1})}^{2}$
$= \frac{2 b^{2}}{cos θ + 1} - \frac{b^{2} sin θ}{{(cos θ + 1)}^{2}}$
$= \frac{b^{2}}{cos θ + 1} \frac{b^{2} sin θ}{{(cos θ + 1)}^{2}}$
$= \frac{b^{2}}{cos θ + 1} (\frac{2 cos θ + 2 - {sin}^{2} θ}{cos θ + 1})$
$= \frac{b^{2}}{cos θ + 1} (\frac{2 cos θ + 1 + {cos}^{2} θ}{cos θ + 1}) = b^{2} = 4$

|

Updated on:21/07/2023

Class 12 MATHS QUESTION BANK

Similar Questions

Recommended Questions

Home
Ask Doubt
Profile