Question

Let $P$
be any point on a directrix of an ellipse of eccentricity $e,S$
be the corresponding focus, and $C$
the center of the ellipse. The line $PC$
meets the ellipse at $A\stackrel{.}{}$
The angle between $PS$
and tangent a $A$
is $\alpha$
. Then $\alpha$
is equal to
${\tan }^{-1}e$

(b) $\frac{\pi }{2}$

${\tan }^{-1}(1-e^2)$
(d) none of these

Options

A. `tan^(-1)e`
B. `pi//2`
C. `tan^(-1)(1-e^(2))`
D. none of these

Explanation

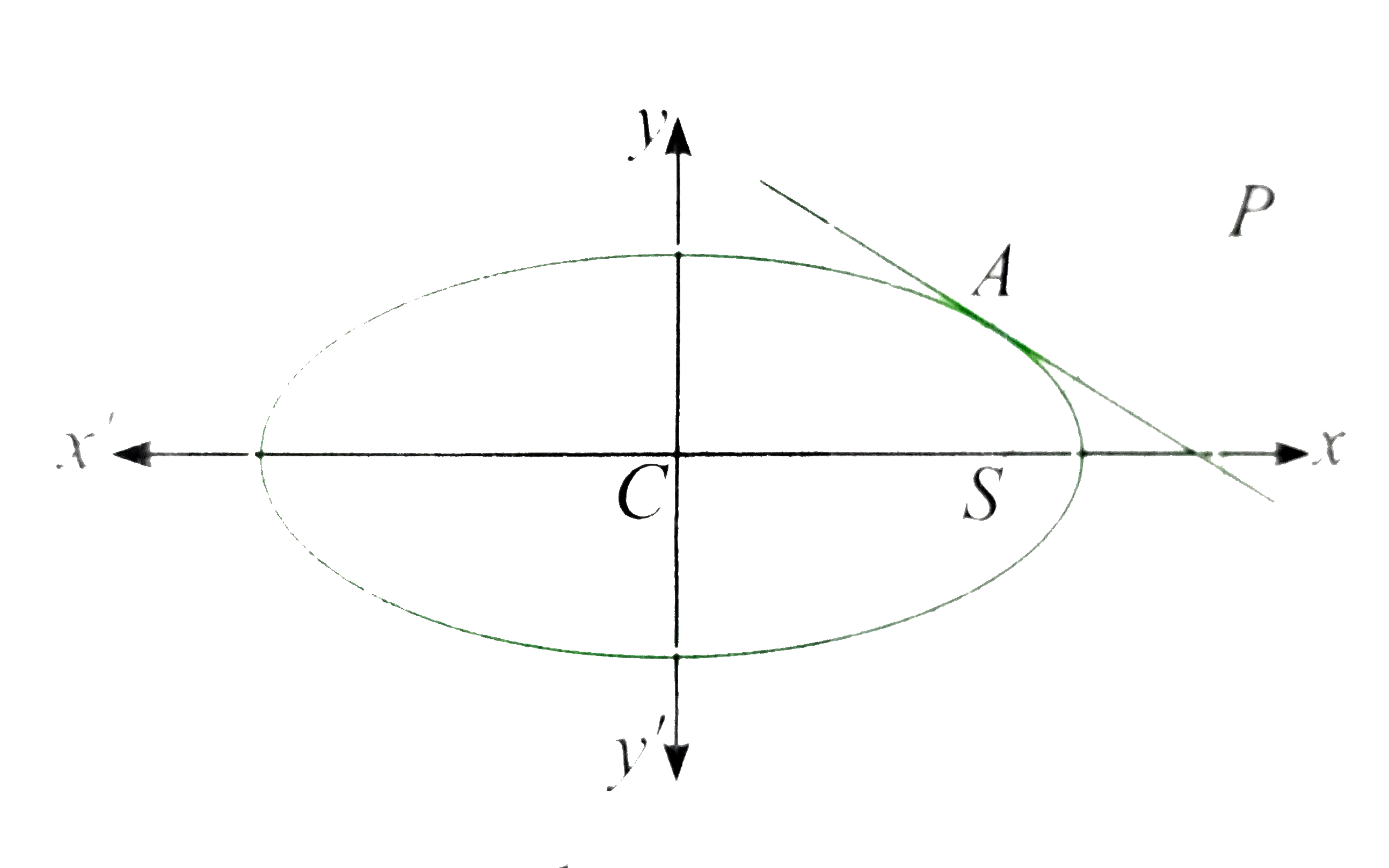
Let the ellipse be
`(x^(2))/(a^(2))+(y^(2))/(b^(2))=1`
and let `A-=(a cos theta, b sin theta)`
The equation of AC will be
`y=(b)/(a) tan thetax`
Solving with x=a/e, we get
`P-=((a)/(e)(b)/(e) tan theta)`
Slop of tangent at `A=-(b)/(a tan theta)`
Slope of `PS=((b)/(e) tantheta)/((a)/(e)-ae)=(b tantheta)/(a(1-e^(2)))=(a)/(b)tan theta`
So, `alpha=(pi)/(2)`