The line x+2y=1 cuts the ellipse 1 at two distinct points A and B. Point C is on the ellipse such that area of triangle ABC is maximum, then find point C.Solution in Bengali
The correct Answer is:
, which is required locus.
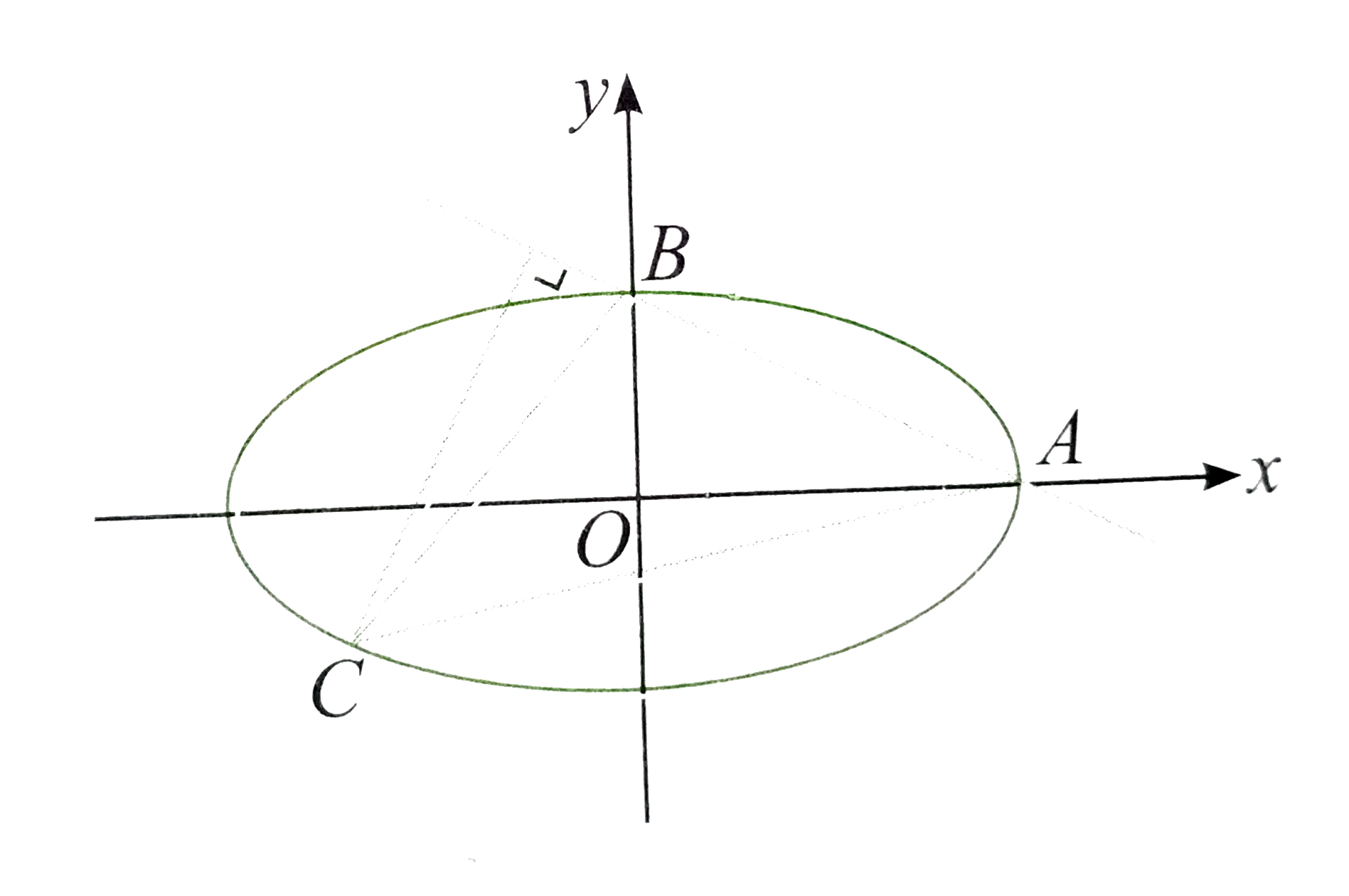
Clearly, line x+2y=1 cuts the ellipse at .
Let point C on the ellipse be
Now, are of the triangle ABC is maximum, if distance of C from AB is maxiumm
Distance of C from AB,
Maximum value of d occur when
Similar Questions
A tangent to the ellipse x24+y21=1 cuts the circle x2+y2=4 at point A and B C is any point on the circle x2+y4=4 such that A, B and C are to the same side of x-axis find the maximum , area of the traingle ABC.
View SolutionThe line x=t2 meet the ellipse x2+y29=1 in the real and distinct points if and only if
View SolutionThe ratio of the area of triangle inscribed in ellipse x2a2+y2b2=1 to that of triangle formed by the corresponding points on the auxiliary circle is 0.5. Then, find the eccentricity of the ellipse. (A) 12 (B) √32 (C) 1√2 (D) 1√3
View SolutionA tangent having slope of −43 to the ellipse x218+y232=1 intersects the major and minor axes at points A and B, respectively. If C is the center of the ellipse, then find area of triangle ABC.
View SolutionThe line x+2y=1 cuts the ellipse x2+4y2=1 1 at two distinct points A and B. Point C is on the ellipse such that area of triangle ABC is maximum, then find point C.
View SolutionEquation of the ellipse is x2a2+y2b2=1 with foci S1andS2 The maximum area of the triangle PS1S2, where P is any point on the ellipse is
View SolutionThe ratio of the area of triangle inscribed in ellipse x2a2+y2b2=1 to that of triangle formed by the corresponding points on the auxiliary circle is 0.5. Then, find the eccentricity of the ellipse. (A) 12 (B) √32 (C) 1√2 (D) 1√3
View SolutionA tangent having slope of -4/3 to the ellipse (x^2)/(18)+(y^2)/(32)=1 intersects the major and minor axes at points A and B , respectively. If C is the center of the ellipse, then find area of triangle A B Cdot
View Solution