Question

A region in the $x-y$
plane is bounded by the curve $y=\sqrt{25-x^2}$
and the line $y=0$
. If the point $(a,a+1)$
lies in the interior of the region, then
(a)$a\in (-4,3)$
(b) $a\in (-\infty ,-1)$ ∪ $(3,\infty )$

(c)$a\in (-1,3)$
(d) none of these

Options

A. `a in (-4,3)`
B. `a in (- oo,-1) in (3, oo)`
C. `a in (-1),3)`
D. none of these

Answer

3

Explanation

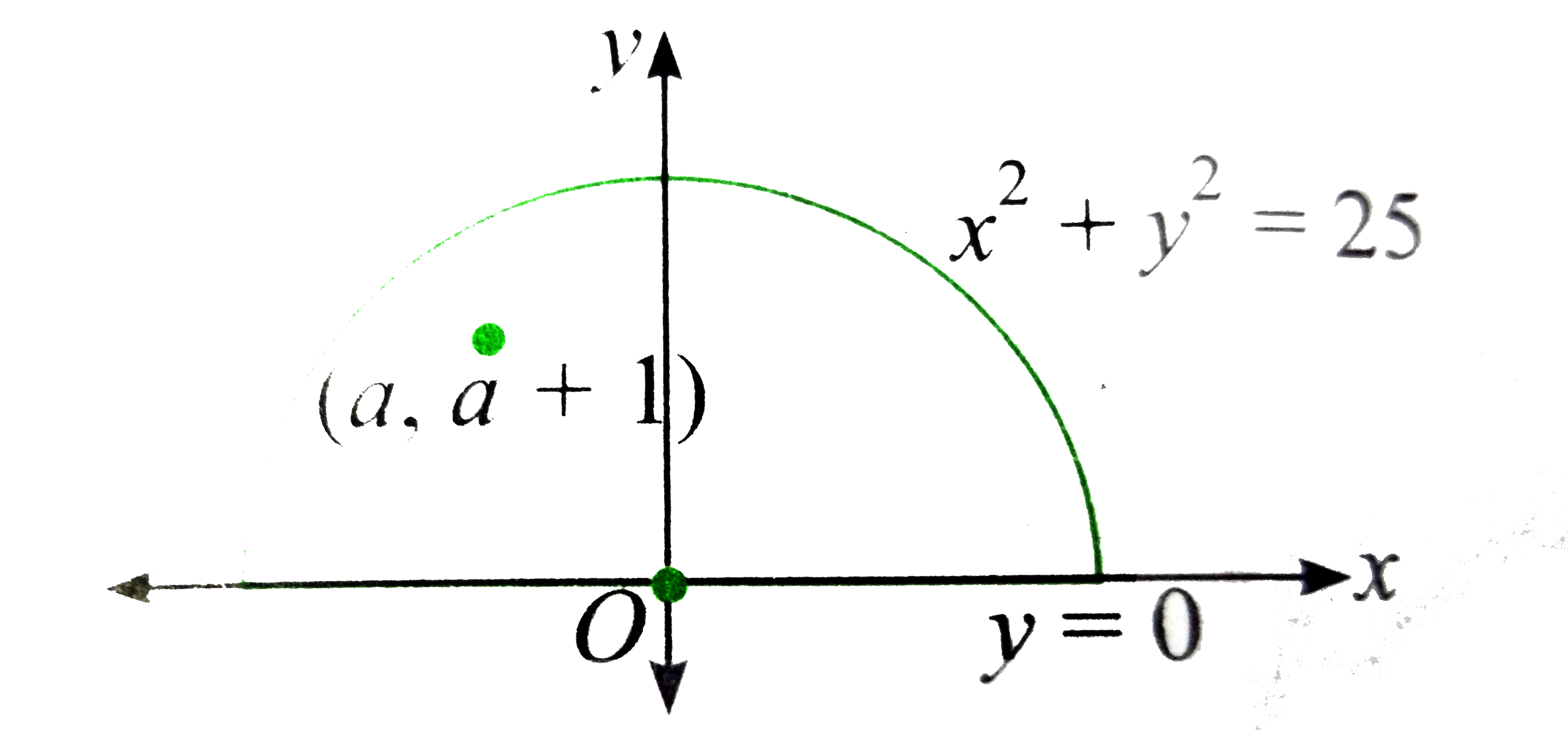
`y=sqrt(25-x^(2))` and `y=0` bound the semicircle above the x-axis .
Therefore,
`a+1gt0` (1)
and `a^(2)+(a+1)^(2)-25lt0` or `2a^(2)+2a-24lt0`
or `a^(2)+a-12 lt0`
or `-4 lta lt3` (2)
From (1) and (2),
`-1 lta lt3`