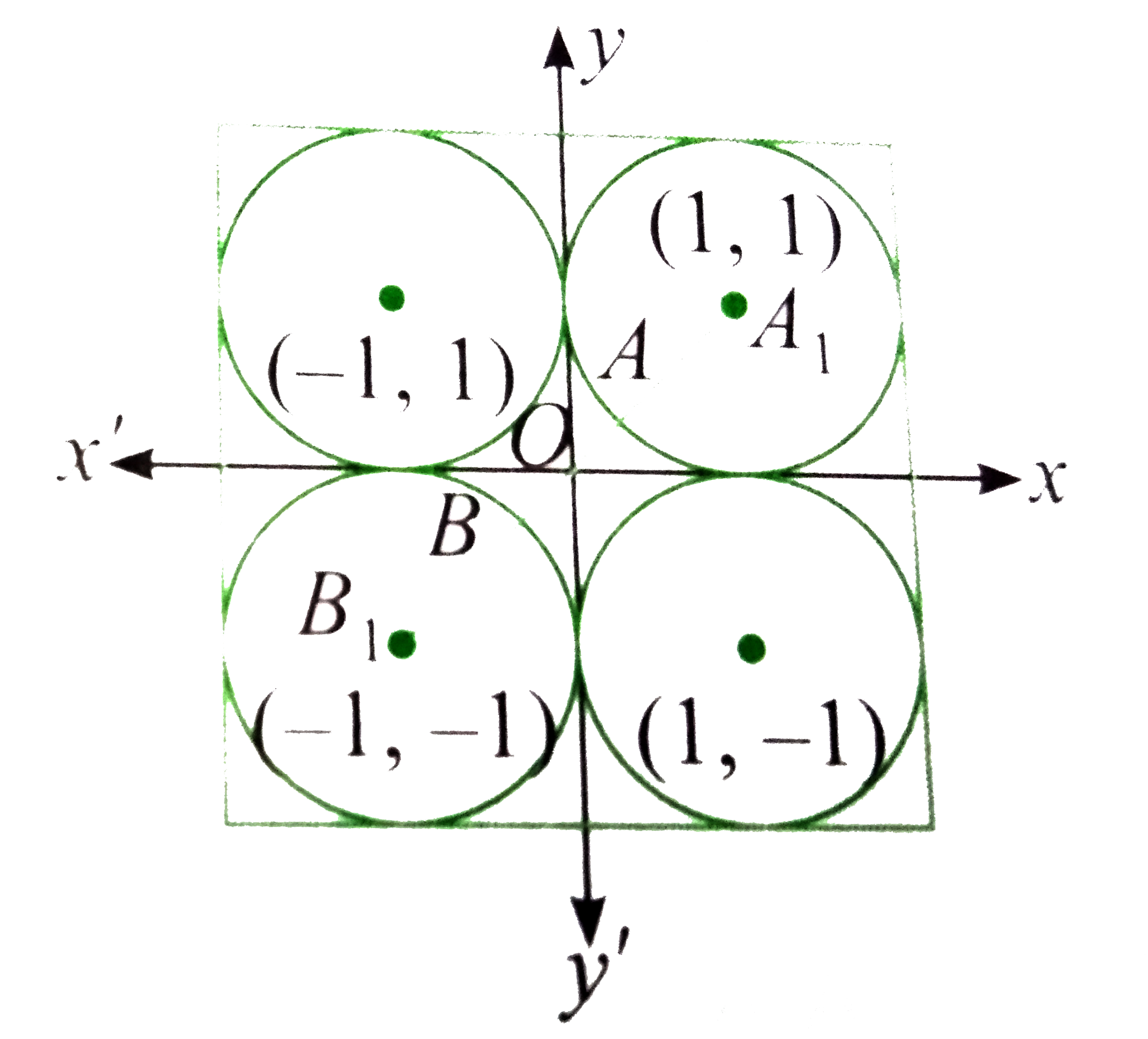
Consider four circles (x±1)2+(y±1)2=1 . Find the equation of the smaller circle touching these four circles.Solution in Bengali
The correct Answer is:x2+y2=3−2√2
A1B1=√4+4=2√2
∴AB=2√2−2=2(√2−1)
Thus, the equation of the required circle isx2+y2=(√2−1)2=3−2√2
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - CONCEPT APPLICATION EXERCISE 4.13
4 Videos
- CIRCLE BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - CONCEPT APPLICATION EXERCISE 4.14
4 Videos
- CIRCLE BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - CONCEPT APPLICATION EXERCISE 4.11
4 Videos
- BINOMIAL THEOREMBOOK - CENGAGE PUBLICATIONCHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension
11 Videos
- CIRCLESBOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLESEXERCISE - Comprehension Type
8 Videos
Similar Questions
Prove that the locus of the centroid of the triangle whose vertices are (acost,asint),(bsint,−bcost), and (1,0) , where t is a parameter, is circle.
View SolutionFind the locus of center of circle of radius 2 units, if intercept cut on the x-axis is twice of intercept cut on the y-axis by the circle.
View SolutionProve that the locus of the point that moves such that the sum of the squares of its distances from the three vertices of a triangle is constant is a circle.
View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is
View Solution
In the diagram as shown, a circle is drawn with centre C(1,1) and radius 1 and a line L. The line L is tangent to the circle at Q. Further L meets the y-axis at R and the x-axis at P in such a way that the angle OPQ equals θ where 0<θ<π2.
Coordinate of Q is
View SolutionConsider four circles (x±1)2+(y±1)2=1 . Find the equation of the smaller circle touching these four circles.
View SolutionThe equation of four circles are (x±a)2+(y±a2=a2 . The radius of a circle touching all the four circles is (√2+2)a (b) 2√2a (√2+1)a (d) (2+√2)a
View SolutionEquation of the smaller circle that touches the circle x^(2)+y^(2)=1 and passes through the point (4,3) is
View SolutionThe equation of the four circles are (x±a)2+(y±a)2=a2. The radius of the smallest circle, which touches all the four circles, is:
View SolutionThere are four circles each of radius 1 unit touching both the axis. The equation of the smaller circle touching all these circle is
View SolutionEquation of the smaller circle that touches the circle x2+y2=1 and passes through the point (4,3) is
View SolutionConsider four circles (x±1)2+(y±1)2=1 . Find the equation of the smaller circle touching these four circles.
View SolutionFind the equation of a circle with center (4, 3) touching the circle x2+y2=1
View SolutionThe equation of four circles are (x±a)2+(y±a2=a2 . The radius of a circle touching all the four circles is (√2+2)a (b) 2√2a (√2+1)a (d) (2+√2)a
View Solutionचार वृत्तों का समीकरण (x±a)2+(y±a)2=a2 है चारों वृत्तों को स्पर्श करने वाले वृत्त की त्रिज्या है
View Solutionचार वृत्तों का समीकरण (x±a)2+(y±a)2=a2 है चारों वृत्तों को स्पर्श करने वाले वृत्त की त्रिज्या है
View Solution
