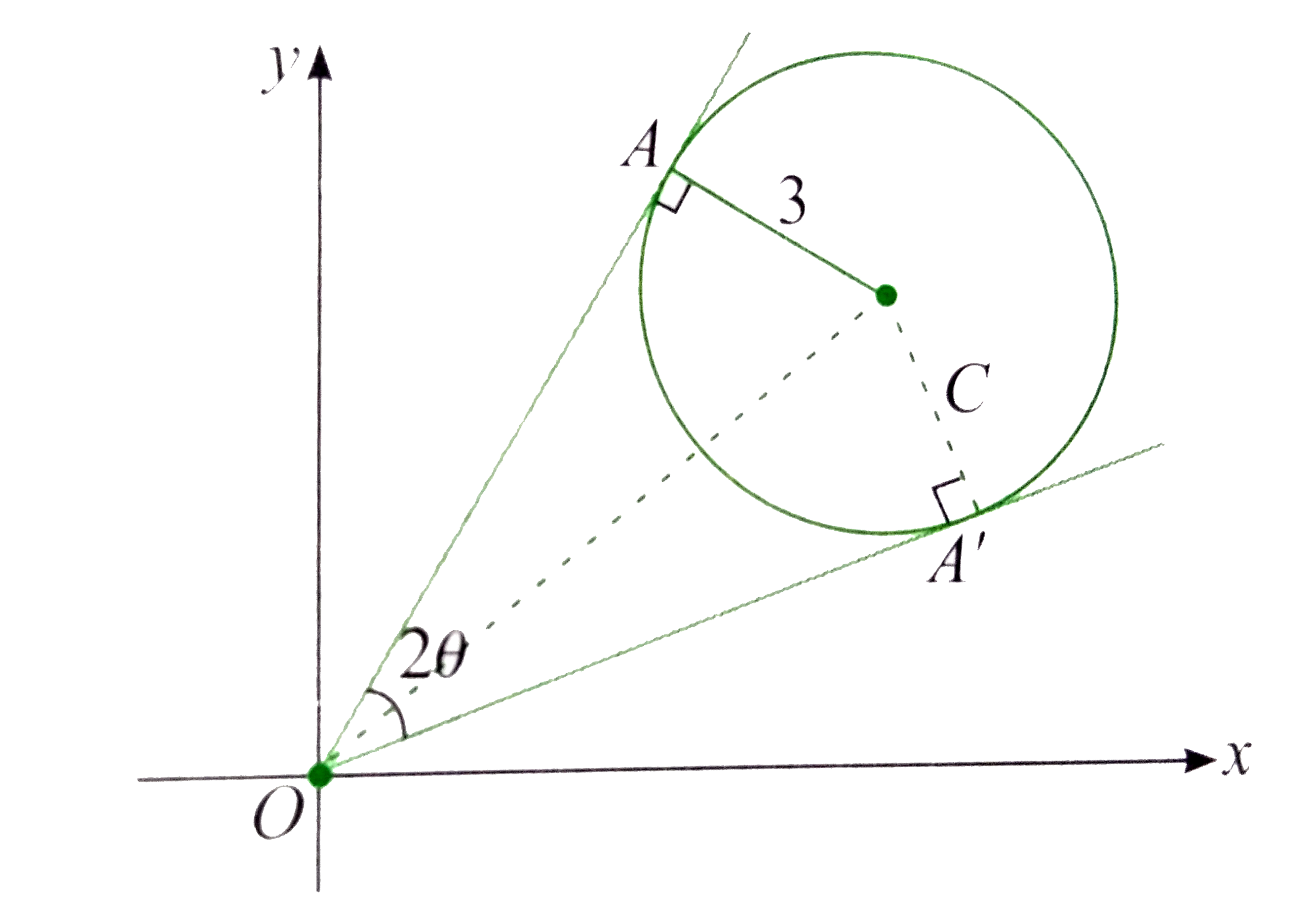
Let 2x2+y2−3xy=0 be the equation of pair of tangents drawn from the origin to a circle of radius 3, with center in the first quadrant. If A is the point of contact. Find OASolution in Bengali
The correct Answer is:3(3+√10)
The equation o2x2−3xy+y2=0 represents a pair of tangents OA and OA'.
Let the angle between these two tangents be 2θ. Then,
tan2θ=2√(−3/2)2−2×12+1
or 2tanθ1−tan2θ=13
or tan2θ+6tanθ−1=0
or tanθ=−6±√36+42=−3±√10
Now, we know that the line joining the point through which tangents are drawn to the center bisects the angle between the tangents. Therefore,
∠AOC=θ
In ΔOAC,
tanθ=3OA
or OA=3√10−3×√10+3√10+3
∴OA=3(3+√10)
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - CONCEPT APPLICATION EXERCISE 4.14
4 Videos
- CIRCLE BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - CONCEPT APPLICATION EXERCISE 4.18
1 Videos
- CIRCLE BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - CONCEPT APPLICATION EXERCISE 4.12
4 Videos
- BINOMIAL THEOREMBOOK - CENGAGE PUBLICATIONCHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension
11 Videos
- CIRCLESBOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLESEXERCISE - Comprehension Type
8 Videos
Similar Questions
Find the locus of center of circle of radius 2 units, if intercept cut on the x-axis is twice of intercept cut on the y-axis by the circle.
View SolutionFind the middle point of the chord of the circle x2+y2=25 intercepted on the line x−2y=2
View SolutionNumber of integral values of λ for which x2+y2+7x+(1−λ)y+5=0 represents the equation of a circle whose radius cannot exceed 5 is
View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is
View Solution
In the diagram as shown, a circle is drawn with centre C(1,1) and radius 1 and a line L. The line L is tangent to the circle at Q. Further L meets the y-axis at R and the x-axis at P in such a way that the angle OPQ equals θ where 0<θ<π2.
Coordinate of Q is
View SolutionLet 2x^(2)+y^(2)-3xy=0 be the equation of pair of tangents drawn from the origin to a circle of radius 3, with center in the first quadrant.If A is the point of contact.Find OA
View SolutionA pair of tangents are drawn from the origin to the circle x2+y2+20(x+y)+20=0 . Then find its equations.
View SolutionLet 2x2+y2−3xy=0 be the equation of a pair of tangents drawn from the origin O to a circle of radius 3 with centre in the first quadrant. If A is one of the points of contact, then the length of OA is
View SolutionA pair of tangents are drawn from the origin to the circle x^(2)+y^(2)+20(x+y)+20=0, The equation of pair of tangent is
View SolutionFind the equation to the chord of contact of the tangents drawn from an external point (−3,2) to the circle x2+y2+2x−3=0.
View Solutionमाना 2x2+y2−3xy मूलबिन्दु से त्रिज्या 3 के वृत्त पर खींची गति स्पर्शी युग्म का समीकरण है, जिसका केंद्र प्रथम चतुथार्श में है। यदि A एक स्पर्श बिन्दु है तो OA की लम्बाई ज्ञात कीजिए।
View Solutionवृत्त जिसका केन्द्र (2,-1) है, पर मूलबिन्दु से खींची गयी एक स्पर्श रेखा का समीकरण 3x + y= 0 हो, तो दूसरी स्पर्श रेखा का समीकरण है
View SolutionLet 2x2+y2−3xy=0 be the equationof a pair of tangents drawn from the orign O to a circlke of radius 3 with centre in the first quadrant. If A is one of the point of contact then show that the length of OA is 3(3+√10.
View SolutionA pair of tangents are drawn from the origin to the circle x2+y2+20(x+y)+20=0 . Then find its equations.
View SolutionLet 2x2+y2−3xy=0 be the equation of pair of tangents drawn from the origin to a circle of radius 3, with center in the first quadrant. If A is the point of contact. Find OA
View SolutionLet 2x2+y2−3xy=0 be the equation of pair of tangents drawn from the origin to a circle of radius 3, with center in the first quadrant. If A is the point of contact. Find OA
View Solution
