Two variable chords ABandBC of a circle x2+y2=r2 are such that AB=BC=r . Find the locus of the point of intersection of tangents at AandC.Solution in Bengali
The correct Answer is:x2+y2=4r2
Let the point of intersection of tangents at A and be P≡(x,y) .
Since AB=AO=BO=r, we get
∠AOB=60∘
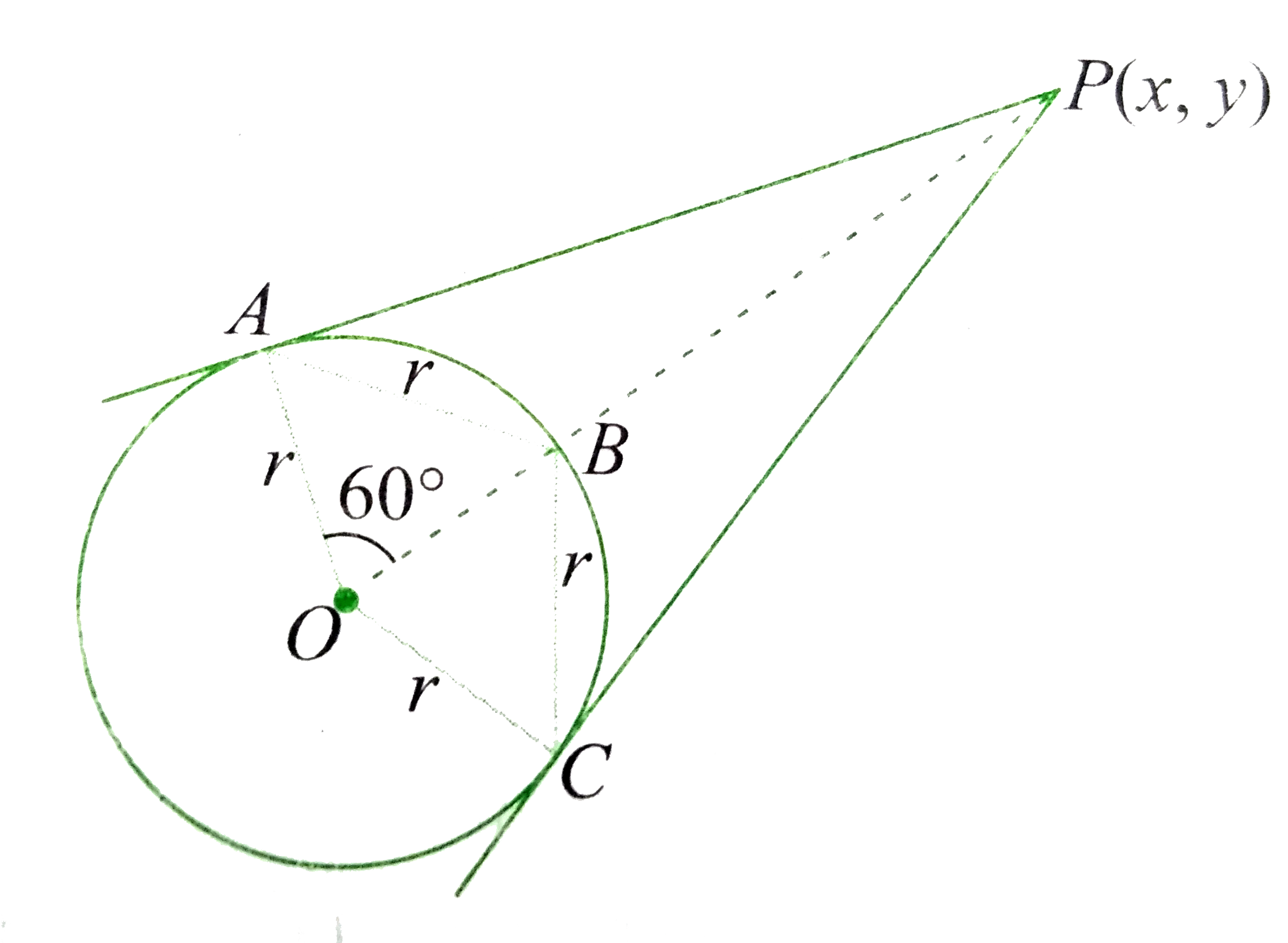
or PArtan60∘=√3
or √x2+y2−r2=√3r
Therefore, x2+y2=4r2 is the locus of the point P.
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - CONCEPT APPLICATION EXERCISE 4.16
3 Videos
- CIRCLE BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - CONCEPT APPLICATION EXERCISE 4.17
2 Videos
- CIRCLE BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - CONCEPT APPLICATION EXERCISE 4.20
1 Videos
- BINOMIAL THEOREMBOOK - CENGAGE PUBLICATIONCHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension
11 Videos
- CIRCLESBOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLESEXERCISE - Comprehension Type
8 Videos
Similar Questions
If the circle x2+y2−4x−8y−5=0 intersects the line 3x−4y=m at two distinct points, then find the values of m.
View SolutionThree concentric circles of which the biggest is x2+y2=1, have their radii in A.P If the line y=x+1 cuts all the circles in real and distinct points. The interval in which the common difference of the A.P will lie is:
View SolutionThrough a fixed point (h,k), secant are drawn to the circle x2+y2=r2. Show that the locus of the midpoints of the secants by the circle is x2+y2=hx+ky.
View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is
View Solution
In the diagram as shown, a circle is drawn with centre C(1,1) and radius 1 and a line L. The line L is tangent to the circle at Q. Further L meets the y-axis at R and the x-axis at P in such a way that the angle OPQ equals θ where 0<θ<π2.
Coordinate of Q is
View SolutionTwo circles with centres AandB of radii 3cmand4cm respectively intersect at two points CandD such that ACandBC are tangents to the two circles. Find the length of the common chord CD.
View SolutionThe tangent at any point P on the circle x2+y2=4 meets the coordinate axes at AandB . Then find the locus of the midpoint of AB.
View SolutionTwo variable chords ABandBC of a circle x2+y2=r2 are such that AB=BC=r . Find the locus of the point of intersection of tangents at AandC.
View SolutionLet aandb be nonzero real numbers. Then the equation (ax2+by2+c)(x2−5xy+6y2)=0 represents. four straight lines, when c=0 and a,b are of the same sign. two straight lines and a circle, when a=b and c is of sign opposite to that a two straight lines and a hyperbola, when aandb are of the same sign and c is of sign opposite to that of a a circle and an ellipse, when aandb are of the same sign and c is of sign opposite to that of a
View SolutionThe chords of contact of tangents from three points A,BandC to the circle x2+y2=a2 are concurrent. Then A,BandC will (a)be concyclic (b) be collinear (c)form the vertices of a triangle (d)none of these
View SolutionTwo variable chords ABandBC of a circle x2+y2=r2 are such that AB=BC=r . Find the locus of the point of intersection of tangents at AandC.
View SolutionIf the tangents to the parabola y2=4ax intersect the hyperbola x2a2−y2b2=1 at AandB , then find the locus of the point of intersection of the tangents at AandB.
View SolutionLet aandb be nonzero real numbers. Then the equation (ax2+by2+c)(x2−5xy+6y2)=0 represents. four straight lines, when c=0 and a,b are of the same sign. two straight lines and a circle, when a=b and c is of sign opposite to that a two straight lines and a hyperbola, when aandb are of the same sign and c is of sign opposite to that of a a circle and an ellipse, when aandb are of the same sign and c is of sign opposite to that of a
View SolutionTwo variable chords ABandBC of a circle x2+y2=r2 are such that AB=BC=r . Find the locus of the point of intersection of tangents at AandC.
View SolutionThe chords of contact of tangents from three points A,BandC to the circle x2+y2=a2 are concurrent. Then A,BandC will be
View SolutionTwo circles with centres AandB of radii 3cmand4cm respectively intersect at two points CandD such that ACandBC are tangents to the two circles. Find the length of the common chord CD.
View Solution
