Two parallel tangents to a given circle are cut by a third tangent at the point RandQ . Show that the lines from RandQ to the center of the circle are mutually perpendicular.Solution in Bengali
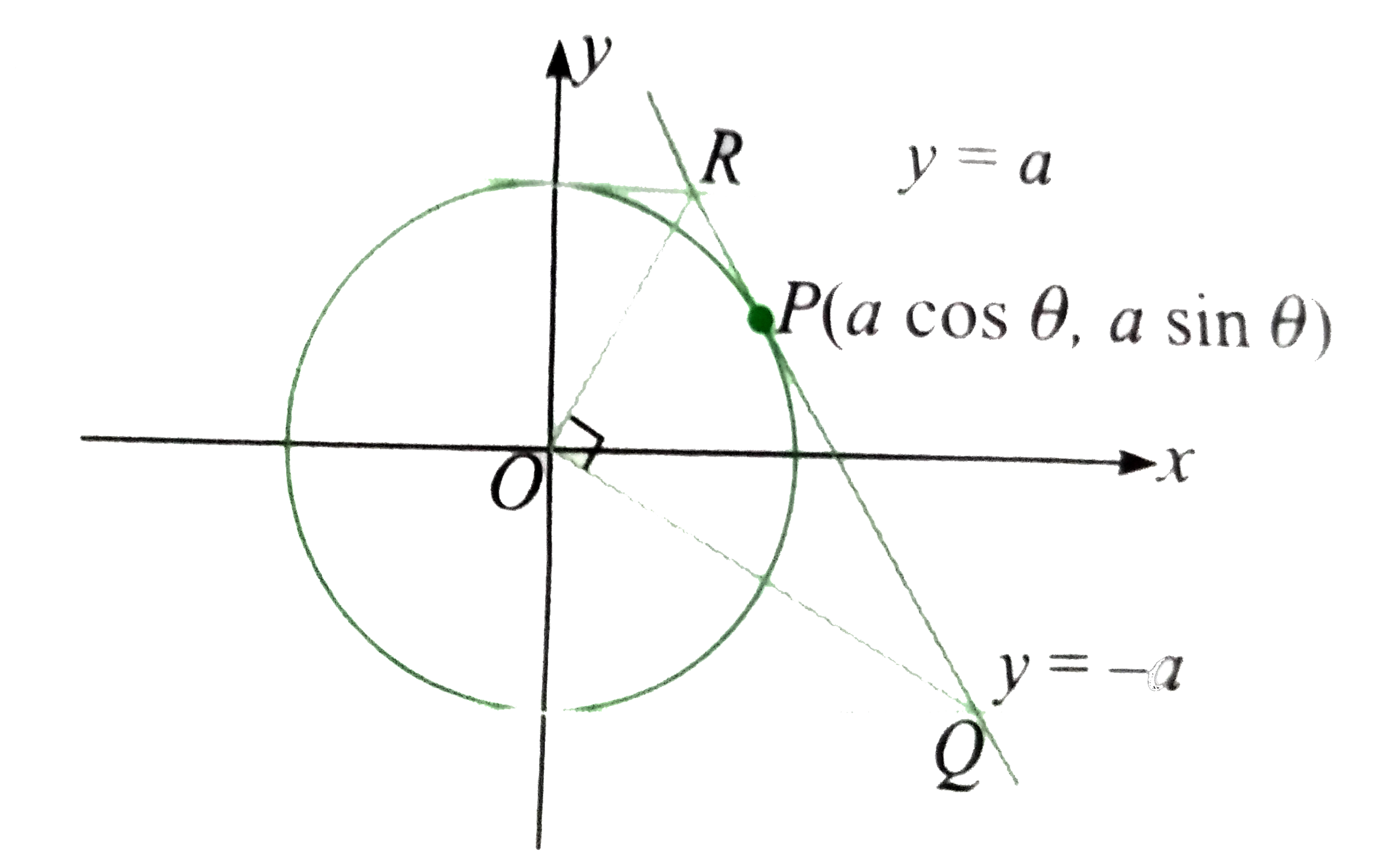
Consider the circle x2+y2=a2.
Let the two parallel tangents be y=a and y=−a.
Third tangent at point P(acosθ,asinθ) is cosθx+sinθy=a.
Solving these with y=±a, we get x=a−+asinθcosθ
∴R≡(a−asinθcosθ,a) and Q≡(a+asinθcosθ,−a)
Slope of OR, m1=aa−asinθcosθ=cosθ1−sinθ
Slope of OQ, m2=−aa+asinθcosθ=−cosθ1+sinθ
m1×m2=cosθ1−sinθ×(−cosθ1+sinθ)=−cos2θ1−sin2θ=−1
Thus, QR subtends right angle at centre.
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - Examples
13 Videos
- CIRCLE BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - CONCEPT APPLICATION EXERCISE 4.1
1 Videos
- BINOMIAL THEOREMBOOK - CENGAGE PUBLICATIONCHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension
11 Videos
- CIRCLESBOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLESEXERCISE - Comprehension Type
8 Videos
Similar Questions
The line Ax+By+C=0 cuts the circle x2+y2+ax+by+c=0 at PandQ . The line A′x+B′x+C′=0 cuts the circle x2+y2+a′x+b′y+c′=0 at RandS. If P,Q,R, and S are concyclic, then show that |a−a'b−b'c−c'ABCA'B'C'|=0
View SolutionIf a circle whose center is (1,−3) touches the line 3x−4y−5=0 , then find its radius.
View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is
View Solution
In the diagram as shown, a circle is drawn with centre C(1,1) and radius 1 and a line L. The line L is tangent to the circle at Q. Further L meets the y-axis at R and the x-axis at P in such a way that the angle OPQ equals θ where 0<θ<π2.
Coordinate of Q is
View SolutionTwo parallel tangents to a given circle are cut by a third tangent at the point RandQ . Show that the lines from RandQ to the center of the circle are mutually perpendicular.
View SolutionTwo parallel tangents to a given circle are cut by a third tangent at the points AandB. If C is the center of the given circle, then ∠ACB depends on the radius of the circle. depends on the center of the circle. depends on the slopes of three tangents. is always constant
View Solutionसिद्ध कीजिए कि स्पर्श बिंदु से स्पर्श रेखा पर खींची गया लम्ब वृत्त के केन्द्र से होकर जाता है।
View Solutionसिद्ध कीजिए कि वृत्त कि दो समान्तर स्पर्शियों के स्पर्श बिन्दु को मिलाने वाली रेखा वृत्त का व्यास होती है।
View Solutionचित्र में,l और m, एक वृत्त पर बिंदुओं A और B पर दो समानान्तर स्पर्श रेखाएँ हैं। यदि वृत्त पर बिंदु पर खींची गई स्पर्श रेखा , स्पर्श रेखाओं l और m के बीच DE अन्तः खण्ड काटती हैं और F वृत्त का केंद्र हैं ,तो सिद्ध करो कि ∠DEF=90∘
View SolutionIn the adoining figure, A is the centre of the circle. Poin D is in the exterior of the circle. Line DP and Line DQ are tangents at points at P and Q respectively. Prove that DP=DQ.
View SolutionPerpendiculars are drawn, respectively, from the points PandQ to the chords of contact of the points QandP with respect to a circle. Prove that the ratio of the lengths of perpendiculars is equal to the ratio of the distances of the points PandQ from the center of the circles.
View SolutionTwo parallel tangents to a given circle are cut by a third tangent at the point RandQ . Show that the lines from RandQ to the center of the circle are mutually perpendicular.
View SolutionTwo parallel tangents to a given circle are cut by a third tangent at the points AandB. If C is the center of the given circle, then ∠ACB (a)depends on the radius of the circle. (b)depends on the center of the circle. (c)depends on the slopes of three tangents. (d)is always constant
View Solutionਸਿੱਧ ਕਰੋ ਕਿ ਸਪਰਸ਼ ਬਿੰਦੂ ਤੋਂ ਸਪਰਸ਼ ਰੇਖਾ 'ਤੇ ਖਿੱਚਿਆ ਗਿਆ ਲੰਬ ਚੱਕਰ ਦੇ ਕੇਂਦਰ ਤੋਂ ਹੋ ਕੇ ਜਾਂਦਾ ਹੈ।
View SolutionIn the picture a triangle is formed by two mutually perpendicular tangents to a circle and a third tangent. Prove that the perimeter of the triangle is equal to the diameter of the circle.
View SolutionThe chord of contact of tangents from a point P to a circle passes through Qdot If l_1a n dl_2 are the length of the tangents from Pa n dQ to the circle, then P Q is equal to
View Solution
