Find the equation of the circle having radius 5 and which touches line 3x+4y−11=0 at point (1, 2).Solution in Bengali
As shown in the figure, the two circles touch the line 3x+4y−11=0 at point (P(1,2).
∴ Centre lies on the line perpendicular to the tangent at P at distance 5 from it on either side.
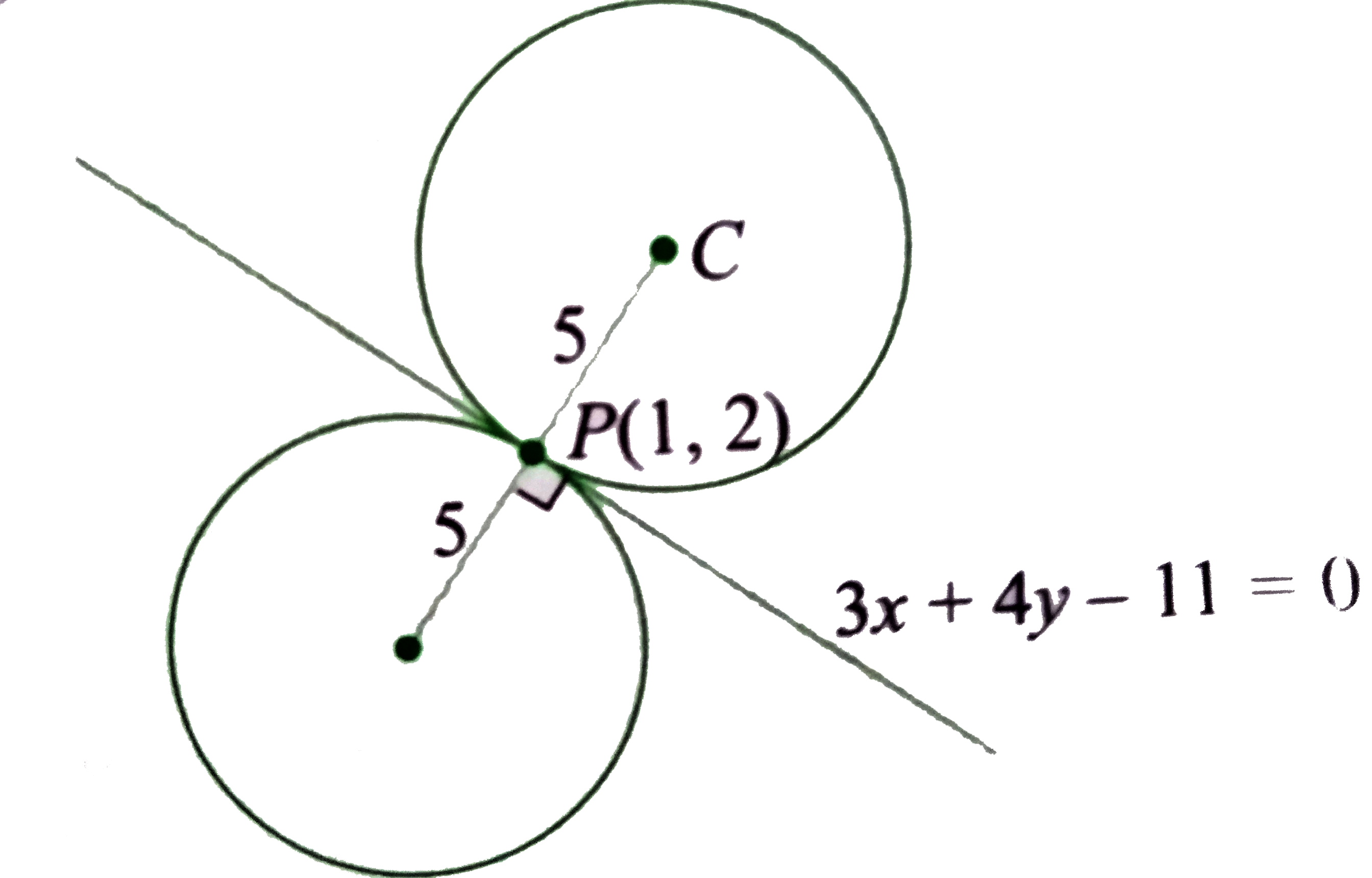
Slope of given tangent line is −34
Thus, the slope of CP is 43.
∴tanθ=43
∴Centre, C≡(1±5cosθ,2±5sinθ)
∴C≡(1±535,2±545)
∴C≡(4,6) or (−2,−2)
Therefore, equations of circles are
(x−4)2+(y−6)2=25
or (x+2)2+(y+2)2=25
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - Examples13videos
CIRCLE
- BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - CONCEPT APPLICATION EXERCISE 4.11videos
CIRCLE
- BOOK - CENGAGE PUBLICATIONCHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension11videos
BINOMIAL THEOREM
- BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLESEXERCISE - Comprehension Type8videos
CIRCLES
Similar Questions
The line Ax+By+C=0 cuts the circle x2+y2+ax+by+c=0 at PandQ . The line A′x+B′x+C′=0 cuts the circle x2+y2+a′x+b′y+c′=0 at RandS. If P,Q,R, and S are concyclic, then show that |a−a'b−b'c−c'ABCA'B'C'|=0
07:26View SolutionIf a circle whose center is (1,−3) touches the line 3x−4y−5=0 , then find its radius.
08:45View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is04:08View Solution
In the diagram as shown, a circle is drawn with centre C(1,1) and radius 1 and a line L. The line L is tangent to the circle at Q. Further L meets the y-axis at R and the x-axis at P in such a way that the angle OPQ equals θ where 0<θ<π2.
Coordinate of Q is09:56View SolutionFind the equation of the circle having radius 5 and which touches line 3x+4y−11=0 at point (1, 2).
04:38View SolutionFind the equation of the circle having radius 5 and touching the line 3x-4y+5=0 at the point (1,2).
05:21View SolutionFind the radius of a circle which touches two lines
3x-4y-6=0 and 6x-8y+1=0.03:49View SolutionFind the equations of the two circles which intersect the circles x2+y2−6y+1=0 and x2+y2−4y+1=0 orthogonally and touch the line 3x+4y+5=0
07:59View SolutionThe equation to the circle with centre (2, 1) and touching the line 3x+4y=5 is...
03:04View SolutionFind the equations of the circles which cut orthogonally the circles x2+y2−6y+1=0,x2+y2−4y+1=0 and touch the line 3x+4y+5=0
04:05View SolutionLocus of the centre of the circle touching the line 3x+4y+1=0 and having radius equal to 5 units is
03:08View SolutionFind the equation of the circle having radius 5 and which touches line 3x+4y−11=0 at point (1, 2).
05:54View SolutionIf a circle whose center is (1,−3) touches the line 3x−4y−5=0 , then find its radius.
05:54View SolutionFind the equation of the circle having radius 5 and which touches line 3x+4y−11=0 at point (1, 2).
05:28View SolutionIf a circle whose center is (1,−3) touches the line 3x−4y−5=0 , then find its radius.
02:20View Solutionकेन्द्र (2, 1) और रेखा 3x+4y=5 को स्पर्श करने वाले वृत्त का समीकरण है
02:34View Solution
