A tangent is drawn at any point on the hyperbola x2a2−y2b2=1. If this tangent is intersected by the tangents at the vertices at points P and Q, then which of the following is/are true Solution in Bengali
S,S',P and Q are concyclic
PQ is diameter of the circle
S,S', P and Q forms rhombus
PQ is diagonal of acute angle of the rhombus formed by S,S',P and Q
The correct Answer is:A, B
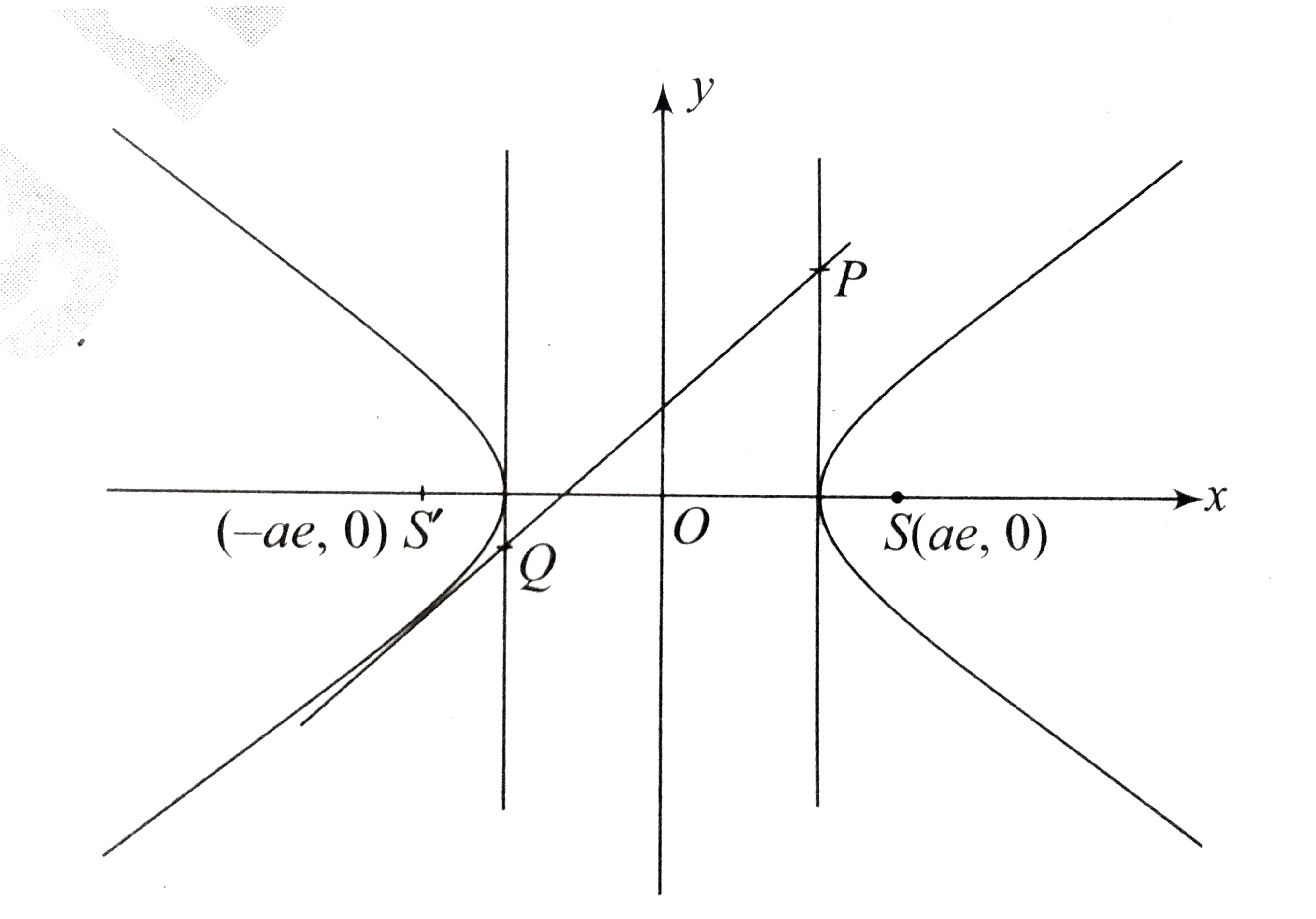
Any tangent to the hyperbola is xsecθa−ytanθb=1 Solving this line with the lines x=±a, we get the coordinates of points P and Q as
(a,btan.θ2) and (−a,−bcot.θ2)
Now slopes of the lines PS and QS are
mPS=btan.θ2a(1−e),mQS=−bcot.θ2−a(1+e)
⇒mPS.mQS=−b2a2(e2−1)=−1
Similarly mPS.mQS'=−1
⇒ line PQ subtends and angle of π2 at S and S'
⇒ points P,Q,S and S' are concyclic.
⇒PQ is diameter.
Similar Questions
From a point P, two tangents PA and PB are drawn to the hyperbola x2a2−y2b2=1. If these tangents cut the coordinates axes at 4 concyclic points, then the locus of P is
View SolutionA tangent is drawn at any point on the hyperbola x2a2−y2b2=1. If this tengent is intersected by the tangents at the vertices at points P and Q then show that S, S' , P and Q are concyclic points where S and S' are the foci of the hyperbola .
View SolutionIf the circle x^(2)+y^(2)=1 A variable tangent of the ellipse x^(2)+2y^(2)=4 Is cut at points P and Q. Then the point of intersection of the tangent lines drawn at P and Q is
View SolutionA tangent is drawn at any point on the hyperbola x2a2−y2b2=1. If this tangent is intersected by the tangents at the vertices at points P and Q, then which of the following is/are true
View SolutionTangent are drawn at points P and Q to the hyperbola 4x2−y2=36. They intersects of point T (0, 3). Then area of ΔPTQ =…….. Sq.
View SolutionShow that the tangents drawn at those points of the ellipse x2a+y2b=(a+b), where it is cut by any tangent to x2a2+y2b2=1, intersect at right angles.
View SolutionThe product of the slopes of two tangents drawn to the hyperbola x24−y29=1 is 4 , Then the locus of the point of intersection of the tangent is
View SolutionTangents at any point P is drawn to hyperbola x2a2−y2b2=1 intersects asymptotes at Q and R, if O is the centre of hyperbola then
View Solution
