The distance of two points P and Q on the parabola y2=4ax from the focus S are 3 and 12 respectively. The distance of the point of intersection of the tangents at P and Q from the focus S is Solution in Bengali
8
6
9
12
The correct Answer is:B
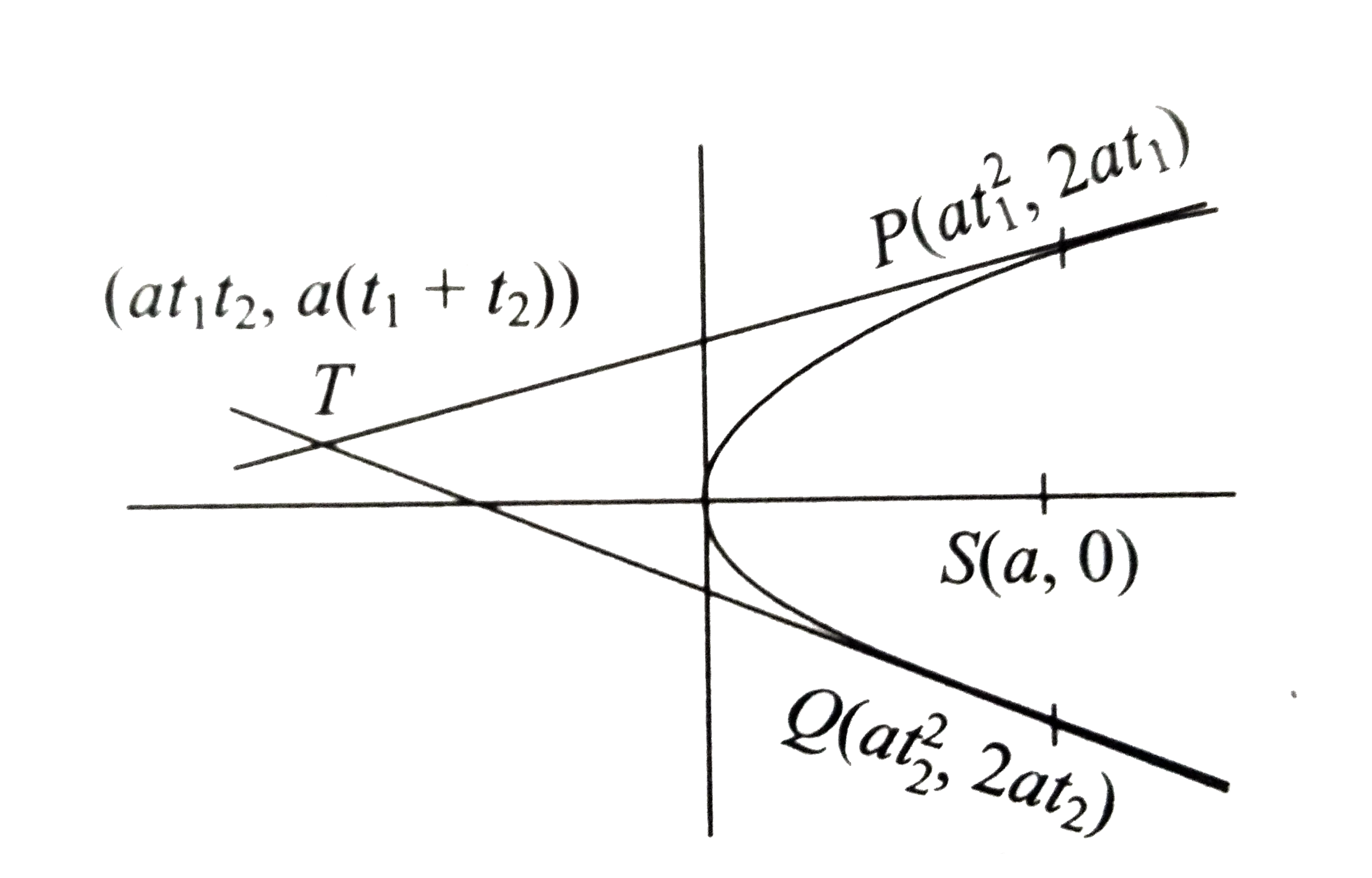
If P(at21,2at1) and Q(at22,2at2), and T(at1t2,a(t1+t2))
Thus, we have ST2=SP×SQ=3×12=36
∴ST=6
Topper's Solved these Questions
- PARABOLABOOK - CENGAGE PUBLICATIONCHAPTER - PARABOLAEXERCISE - Multiple Correct Answers Type
10 Videos
- PARABOLABOOK - CENGAGE PUBLICATIONCHAPTER - PARABOLAEXERCISE - Matching Column Type
1 Videos
- PARABOLABOOK - CENGAGE PUBLICATIONCHAPTER - PARABOLAEXERCISE - Comprehension Type
2 Videos
- PAIR OF STRAIGHT LINESBOOK - CENGAGE PUBLICATIONCHAPTER - PAIR OF STRAIGHT LINESEXERCISE - Numberical Value Type
5 Videos
- PERMUTATION AND COMBINATIONBOOK - CENGAGE PUBLICATIONCHAPTER - PERMUTATION AND COMBINATIONEXERCISE - Comprehension
8 Videos
Similar Questions
A family of curve S is given by S≡x2+2xy+y2−4x(1−λ)−4y(1+λ)+4, then S=0 represents (a) pair of straight line ∀λ∈R (b) straight line for exactly one value of λ (c) parabola ∀λ∈R−{0} (d) ellipse for three values of λ
View SolutionAB is a chord of y2=4x such that normals at A and B intersect at C(9,6) and the tengent at A and B at point T, find (CT)2/13
View SolutionIf cos−1.x2+cos−1.y3=π6, then prove that x24−xy2√3+y29=14
View SolutionThe distance between the lines (x+7y)2+4√2(x+7y)−42=0 is_____________
View SolutionGiven are six 0's, five 1's and four 2's . Consider all possible permutations of all these numbers. [A permutations can have its leading digit 0].
How many permutations have the first 0 preceding the first 1 ?
(a) 15C4×10C5 (b) 15C5×10C4 (c) 15C6×10C5 (d) 15C5×10C5
View SolutionIf the tangent at P on y^(2)=4ax meets the tangent at the vertex in Q and S is the focus of the parabola,then /_SQP is equal to
View SolutionIf the distances of two points P and Q from the focus of a parabola y2=4x are 4 and 9,respectively, then the distance of the point of intersection of tangents at P and Q from the focus is
View SolutionIf the tangent at the extrenities of a chord PQ of a parabola intersect at T, then the distances of the focus of the parabola from the points P.T. Q are in
View SolutionThe distance of two points P and Q on the parabola y2=4ax from the focus S are 3 and 12 respectively. The distance of the point of intersection of the tangents at P and Q from the focus S is
View SolutionAbscissa of two points P and Q on parabola y2=8x are roots of equation x2−17x+11=0. Let Tangents at P and Q meet at point T, then distance of T from the focus of parabola is :
View SolutionIf the distances of two points P and Q on the parabola y2=4ax from the focus of a parabola are 4 and 9 respectively then the distance of the point of intersection of tangents at P and Q from the focus is
View SolutionIf the distances of two points P and Q on the parabola y2=4ax from the focus of a parabola are 4 and 9 respectively then the distance of the point of intersection of tangents at P and Q from the focus is
View SolutionIf the distances of two points P and Q on the parabola y2=4ax from the focus of a parabola are 4 and 9 respectively then the distance of the point of intersection of tangents at P and Q from the focus is
View SolutionAbscissa of two points P and Q on parabola y2=8x are roots of equation x2−17x+11=0. Let Tangents at P and Q meet at point T, then distance of T from the focus of parabola is :
View SolutionIf the distances of two points P and Q on the parabola y2=4ax from the focus of a parabola are 4 and 9 respectively then the distance of the point of intersection of tangents at P and Q from the focus is
View SolutionEquation of the tangent at a point P on the parabola y2=4ax, the normal at which is at a distance a√5/4 from the focus of the parabola is
View Solution
