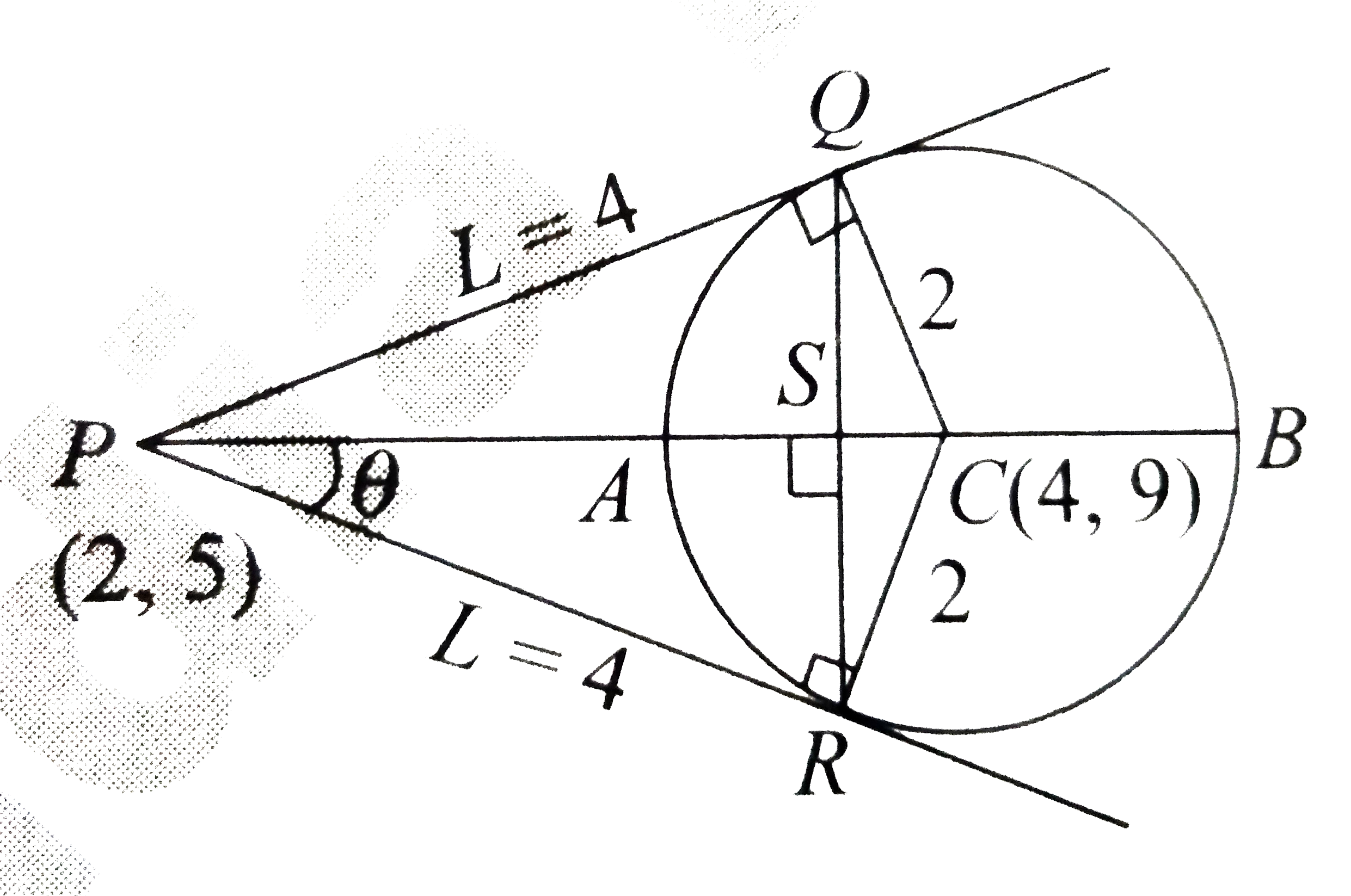
Consider the circle with the center C and a point out side it. From P a pair of tangents PQ and PR are drawn to the circle with S as mid point of QR. The line joining P to C intersects the given circle at A and B. Which of the following hold (s) Solution in Bengali
CP is the arithmetic mean of AP and BP
PR is the geometric mean of PS and PC
PS is the harmonic mean of PA and PB
The angle between the two tangents from P is
The correct Answer is:A, B, C, D
Radius
Thus, CP is the arithmetic mean of AP and BP
Now let,
Also,
Harmonic mean between PA and PB
Thus, PS is the harmonic mean of PA and PB.
Thus, PR is the geometric mean of PS and CP.
Now, angle between the two tangents.
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLESEXERCISE - Comprehension Type8videos
CIRCLES
- BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLESEXERCISE - Comprehension Type8videos
CIRCLES
- BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - For problems 3 and 42videos
CIRCLE
- BOOK - CENGAGE PUBLICATIONCHAPTER - COMPLEX NUMBERSEXERCISE - MULTIPLE CORRECT ANSWER TYPE6videos
COMPLEX NUMBERS
Similar Questions
In the diagram as shown, a circle is drawn with centre C(1,1) and radius 1 and a line L. The line L is tangent to the circle at Q. Further L meets the y-axis at R and the x-axis at P in such a way that the angle OPQ equals θ where 0<θ<π2.
Coordinate of Q is12:58View Solution-
In the diagram as shown, a circle is drawn with centre C(1,1) and radius 1 and a line L. The line L is tangent to the circle at Q. Further L meets the y-axis at R and the x-axis at P in such a way that the angle OPQ equals θ where 0<θ<π2.
Coordinate of Q is09:30View Solution PARAGRAPH X Let S be the circle in the xy -plane defined by the equation x2+y2=4. (For Ques. No 15 and 16) Let E1E2 and F1F2 be the chords of S passing through the point P0(1, 1) and parallel to the x-axis and the y-axis, respectively. Let G1G2 be the chord of S passing through P0 and having slope −1 . Let the tangents to S at E1 and E2 meet at E3 , the tangents to S at F1 and F2 meet at F3 , and the tangents to S at G1 and G2 meet at G3 . Then, the points E3, F3 and G3 lie on the curve x+y=4 (b) (x−4)2+(y−4)2=16 (c) (x−4)(y−4)=4 (d) xy=4
04:02View SolutionLet z1 and z2 be two distinct complex numbers and z=(1−t)z1+tz2, for some real number t with 0<t<1 and i=√−1. If arg(w) denotes the principal argument of a non-zero compolex number w, then
View SolutionConsider the circle x^2+y^2 -8x-18y +93=0 with the center C and a point P(2,5) out side it. From P a pair of tangents PQ and PR are drawn to the circle with S as mid point of QR. The line joining P to C intersects the given circle at A and B. Which of the following hold (s)
06:40View SolutionThe circles x^(2)+y^(2)+2ax-c^(2)=0 and x^(2)+y^(2)+2bx-c^(2)=0 intersect at A and B A line through A meets one circle at P and B parallel line through B meets the other circle at Q.Show that the locus of the mid-point of PQ is a circle.
19:41View SolutionO केंद्र वाले वृत्त पर बिंदु P से PQ स्पर्श रेखा खींची गई हैं और QOR वृत्त का एक व्यास इस तरह हैं की ∠POR=120∘, तब ∠OPQ हैं.।
06:44View Solutionबिंदु P(16,7) से वृत्त x2+y2−2x−4y−20=0 स्पर्श रेखाएं PQ तथा PR खींची गयी हैं। यदि वृत्त का केंद्र c है तो चतुर्भुज PQCR का क्षेत्रफल है-
01:54View Solutionमाना परवलय y2=8x का P एक ऐसा बिंदु है जो वृत्त x2+(y+6)2=1, के केन्द्र C से न्यूनतम दूरी पर है, तो उस वृत्त का समीकरण जो C से होकर जाता है तथा जिसका केन्द्र P पर है, है :
07:21View Solutionகொடுக்கப்பட்ட படத்தில் O மையமாக உடைய வட்டத்தின் ஆரம் 5 செ .மீ ஆகும் .T ஆனது OT =13 செ .மீ என அமைந்த ஒரு புள்ளி மற்றும் OT ஆனது வட்டத்தை E ல் வெட்டுகிறது,வட்டத்தின் E என்ற புள்ளியின் வழியாக செல்லும் ஒரு தொடுகோடு AB எனில் ,AB -யின் நீளம் காண்க ?
04:05View Solutionबिन्दु P (16, 7) से वृत्त x2+y2−2x−4y−20=0 पर स्पर्श रेखायें PQ तथा PR खींची गई हैं। यदि वृत्त का केन्द्र C हो, तो चतुर्भुज PQCR का क्षेत्रफल है।
05:36View Solutionধরো, y2=8x অধিবৃত্তের ওপর P একটি বিন্দু, যা x2+(y+6)2=1 বৃত্তের কেন্দ্র C থেকে ক্ষুদ্রতম দূরত্বে অবস্থিত। এখন, C বিন্দুগামী এবং কেন্দ্র P-তে অবস্থিত বৃত্তের সমীকরণ হবে—
15:38View Solutionধরো , x2+y2=1 বৃত্তের একটি ব্যাস RS, যেখানে S বিন্দুটির স্থানাঙ্ক (1, 0)। ধরো , P একটি চলমান বিন্দু (R এবং S ছাড়া) যা বৃওটির ওপর অবস্থিত এবং S , P বিন্দুতে অঙ্কিত স্পর্শক দুটি পরস্পরকে Q বিন্দুতে ছেদ করে। P বিন্দুতে অঙ্কিত বৃত্তটির অভিলম্ব, Q বিন্দুতে অঙ্কিত RS-এর সমান্তরাল সরলরেখাকে E বিন্দুতে ছেদ করে। E-এর সঞ্চারপথ যে বিন্দু/বিন্দুগুলি দিয়ে যায় তা হল—
04:48View SolutionConsider the circle x2+y2−8x−18y+93=0 with the center C and a point P(2,5) out side it. From P a pair of tangents PQ and PR are drawn to the circle with S as mid point of QR. The line joining P to C intersects the given circle at A and B. Which of the following hold (s)
05:51View Solutionदो स्पर्श रेखायें PQ व PR वृत्त x2+y2−2x−4y−20=0 पर बिन्दु P(16,7) से डाली गयी है, यदि वृत का केन्द्र C हो, तो आकृति PQCR का क्षेत्रफल है
02:17View Solution