Question

Find the minimum integral value of k for which the equation $e^x=k{x}^2$ has exactly three real distinct solutions.

Explanation

Given equation is `e^(x)=kx^(2)`.
`rArr k=e^(x)/x^(2)`
Now let `f(x)=e^(x)/x^(2)`
`therefore f^(')(x) = ((x-2)e^(x))/(x^(3))`
`f^(')(x)=0 therefore x=2`, which is the point of minima.
Also `f(2) =e^(2)/4`
`underset(x to infty)"lim"e^(x)/x^(2)=infty` (using L' Hospital rule twice)
`underset(x to infty) e^(x)/x^(2)=0`
`underset(x to 0)"lim"e^(x)/x^(2)=infty`
Further `f(x) gt 0, AA x in R`.
From this information, the graph of `f(x)` is as shown in the following figure.

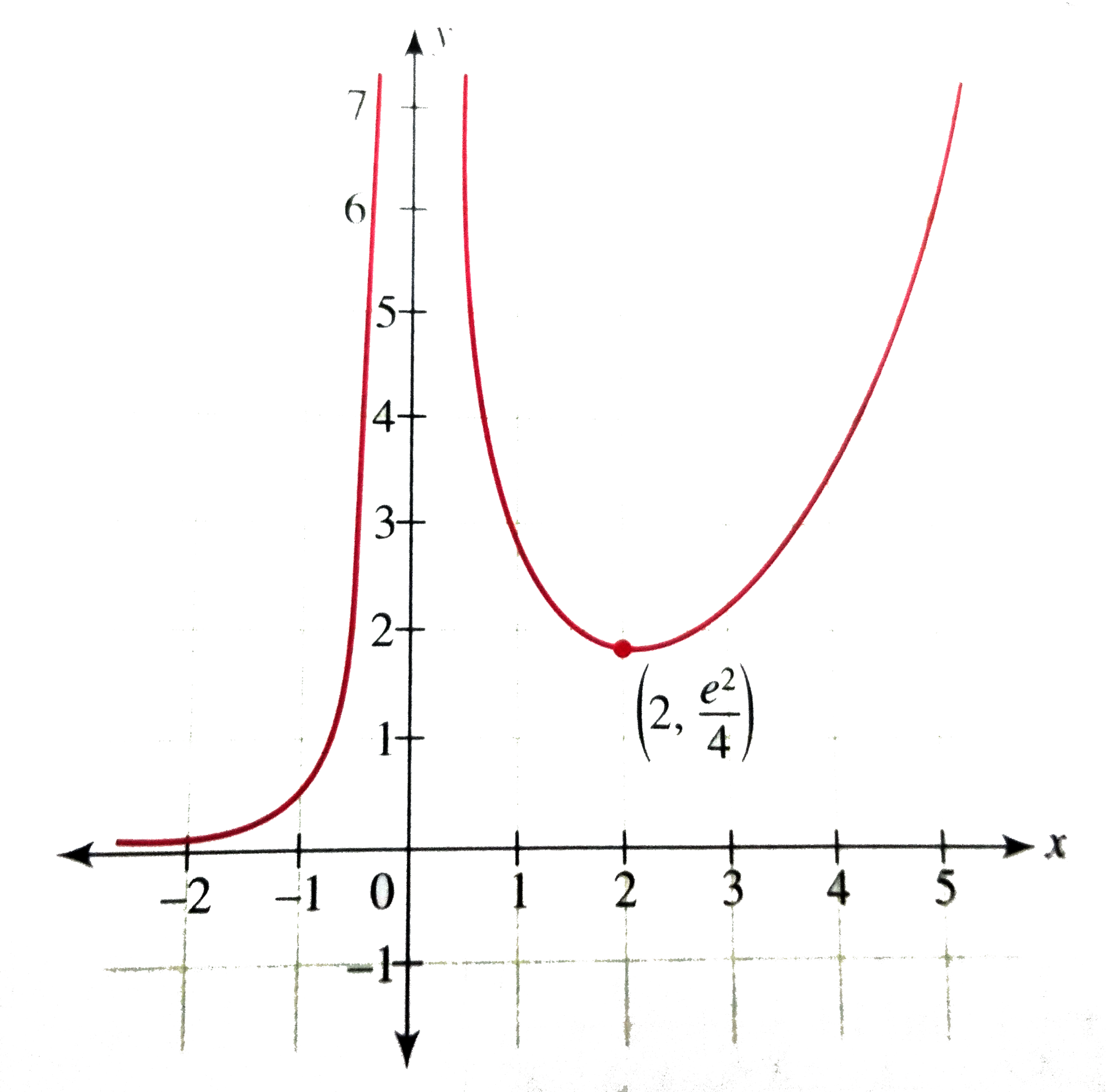
Thus, three real distinct solutions for `k lt e^(2)/4, k in I`.
So, `k_("min") =2`.