The area bounded by the curves y=(log)exandy=((log)ex)2 is Solution in Bengali
e−2 sq. units
3−e sq. units
e sq. units
e−1 sq. units
The correct Answer is:B
Given curves are y=logexandy=(logex)2
Solving logex=(logex)2⇒logex=0,1⇒x=1andx=e
Also, for 1<x<e,0<logex<1⇒logex>(logex)2
For x>e,logex<(logex)2
y=(logex)2>0 for all x>0
and when x→0,(logex)2→∞,
From these information, we can plot the graph of the functions.
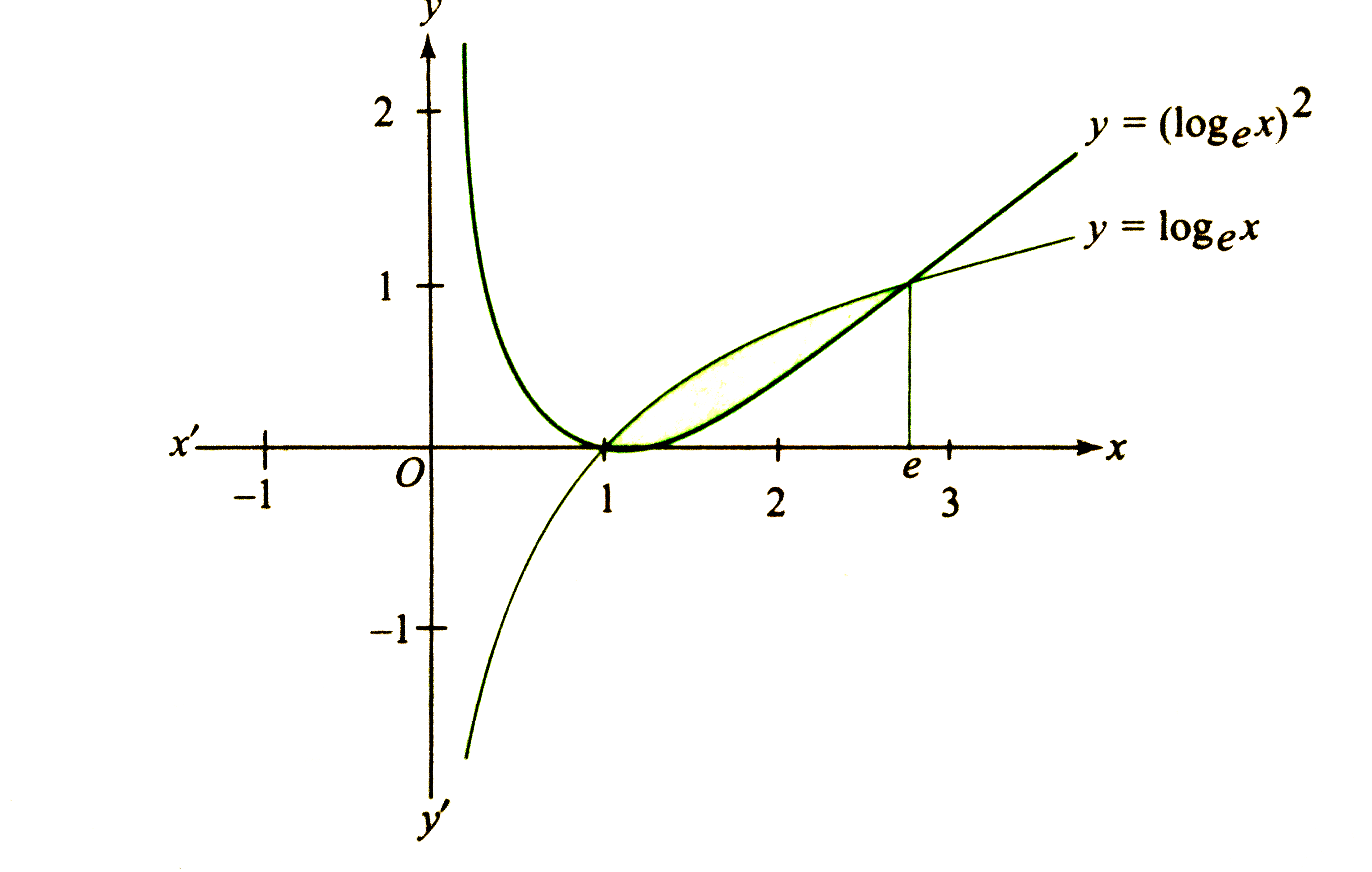
∴ Required area =e∫1(logx−(logex)2)dx
=e∫1logxdx−e∫1(logex)2dx
=[xlogex−x]e1−[x(logex)2]e1+e∫12logexxxdx
=1−e+2[xlogex−x]e1
=3−e sq. units
Topper's Solved these Questions
- AREABOOK - CENGAGE PUBLICATIONCHAPTER - AREAEXERCISE - Multiple Correct Answers Type
13 Videos
- AREABOOK - CENGAGE PUBLICATIONCHAPTER - AREAEXERCISE - Linkded Comprehension Type
21 Videos
- AREABOOK - CENGAGE PUBLICATIONCHAPTER - AREAEXERCISE - Concept Application Exercise 9.3
7 Videos
- APPLICATIONS OF DERIVATIVESBOOK - CENGAGE PUBLICATIONCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Subjective Type
2 Videos
- BINOMIAL THEOREMBOOK - CENGAGE PUBLICATIONCHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension
11 Videos
Similar Questions
Let A(k) be the area bounded by the curves y=x2−3 and y=kx+2 The range of A(k) is (10√53,∞) The range of A(k) is (20√53,∞) If function k→A(k) is defined for k∈[−2,∞ ), then A(k) is many-one function. The value of k for which area is minimum is 1.
View SolutionLet Ar be the area of the region bounded between the curves y2=(e−kr)x(where k>0,r∈N) and the line y=mx(where m≠0), k and m are some constants
A1,A2,A3,… are in G.P. with common ratio
View SolutionFind the continuous function f where (x4−4x2)≤f(x)≤(2x2−x3) such that the area bounded by y=f(x),y=x4−4x2. then y-axis, and the line x=t, where (0≤t≤2) is k times the area bounded by y=f(x),y=2x2−x3,y-axis , and line x=t(where0≤t≤2).
View SolutionProve that for λ>1, the equation xlogx+x=λ has least one solution in [1,λ].
View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is
View SolutionIf y=ax^ax^...((((∞)))) , then prove that dydx=y2(log)eyx(1−y(log)ex(log)ey)
View SolutionPlot the curve y=(log)e(−x).
View SolutionFind the range of f(x)=(log)ex−((log)ex)2∣∣(log)ex∣∣
View SolutionFind the area bounded by (a) y=(log)e|x|andy=0 (b) y=∣∣(log)e∣∣x∣∣andy=0
View SolutionCompute the area of the region bounded by the curves y=ex(log)exandy=logxex
View SolutionThe integrating factor of the differential equation dydx(x(log)ex)+y=2(log)ex is given by
View SolutionPlot the curve y=(log)e(−x).
View SolutionCompute the area of the region bounded by the curves y−ex(log)exandy=logxex
View SolutionFind the area bounded by y=−(log)ex,y=(log)ex,y=(log)e(−x),andy=−(log)e(−x).
View SolutionThe area bounded by the curves y=(log)exandy=((log)ex)2 is
View SolutionThe integrating factor of the differential equation dydx(x(log)ex)+y=2(log)ex is given by
View Solution
