Question

Find the area of the region ${\displaystyle \{(x,y):y^2\le 4x,4x^2+4y^2\le 9\}}$

Answer

`2((9pi)/(16)-(9)/(8) sin^(-1)((1)/(3))+(sqrt(2))/(12))` sq. units

Explanation

Given inequalities are
`y^(2)le4x" (1)"`
`"and "4x^(2)+4y^(2)le9" (2)"`
Points satisfying (1) lies on or in interior to parabola `y^(2)=4x` and those of (2) lies on or inside circle `4x^(2)+4y^(2)=9`
Solving we get,
`4x^(2)+16x=9`
`"or "(2x-1)(2x+9)=0`
`"or "x=1//2` (as x=-9 not possible)
Therefore, the points of intersection of both curves are `((1)/(2),sqrt(2)) and ((1)/(2),-sqrt(2)).`
The graph of these two curves and the common region of the points satisfying both the inequalities is as shown in the fiugre.

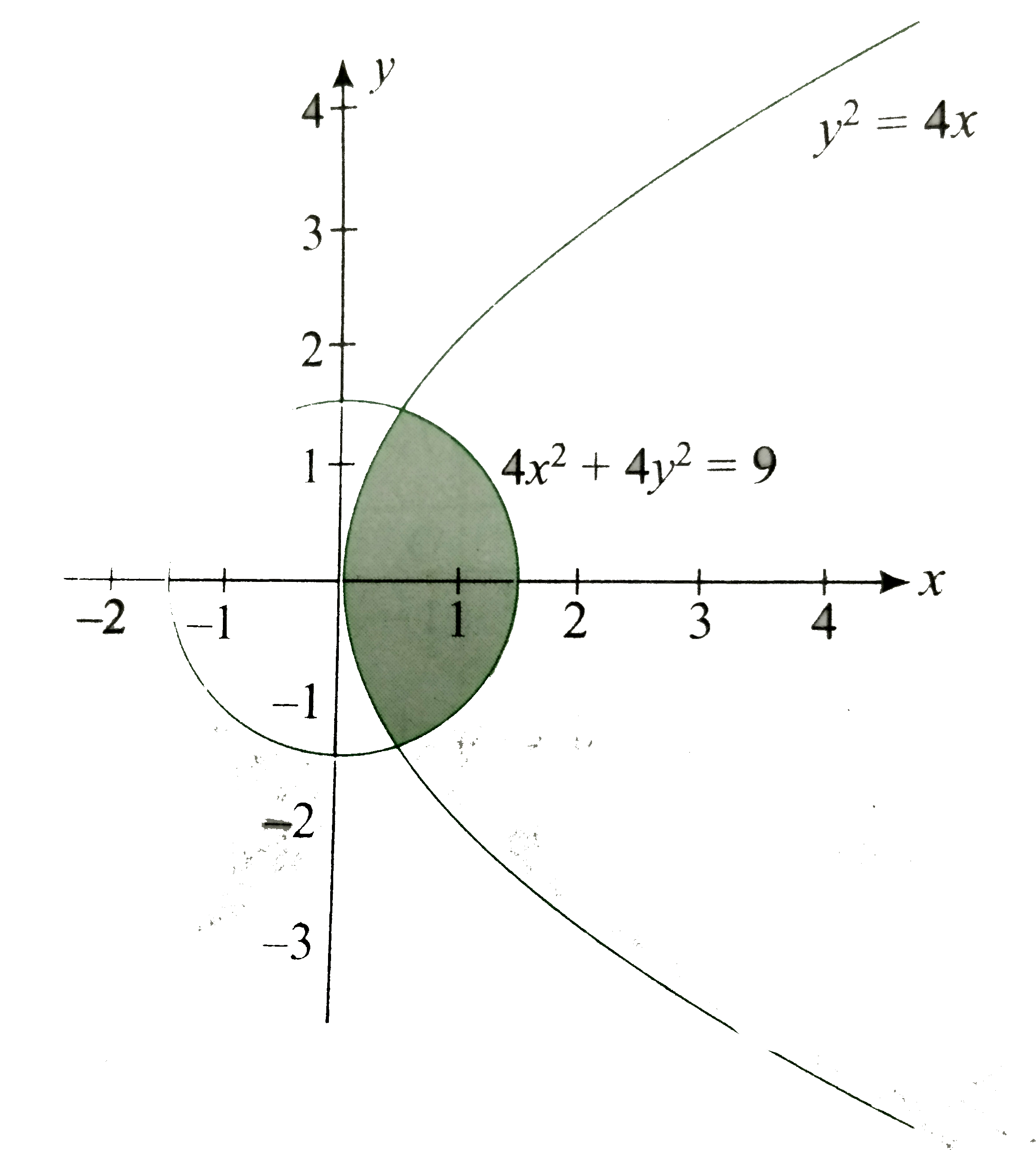
From the figure, required are is given by
`A=2overset((1)/(2))underset(1)int2sqrt(x)dx +2overset((3)/(2))underset((1)/(2))int(1)/(2)sqrt(9-4x^(2))dx`
Putting 2x=t in the second integral, we get
`dx=(dt)/(2)`
`therefore" "A=2[overset((1)/(2))underset(0)int2sqrt(x)dx+(1)/(4)overset(3)underset(1)intsqrt((3)^(2)-(t)^(2))dt]`
`=2([2(x^((3)/(2)))/((3)/(2))]_(0)^((1)/(2))+(1)/(4)[(t)/(2)sqrt(9-t^(2))+(9)/(2)sin^(-1)((t)/(3))]_(1)^(3))`
`=2((2)/(3sqrt(2))+(1)/(4)[{0+(9)/(2)sin^(-1)(1)}-{(1)/(2)sqrt(8)+(9)/(2)sin^(-1)((1)/(3))}])`
`=2((9pi)/(16)-(9)/(8)sin^(-1)((1)/(3))+(sqrt(2))/(12))`