Prove that area common to ellipse x2a2+y2b2=1 and its auxiliary circle x2+y2=a2 is equal to the area of another ellipse of semi-axis a and a-b.Solution in Bengali
We have ellipse x2a2+y2b2=1.
∴ y=±b√1−x2a2
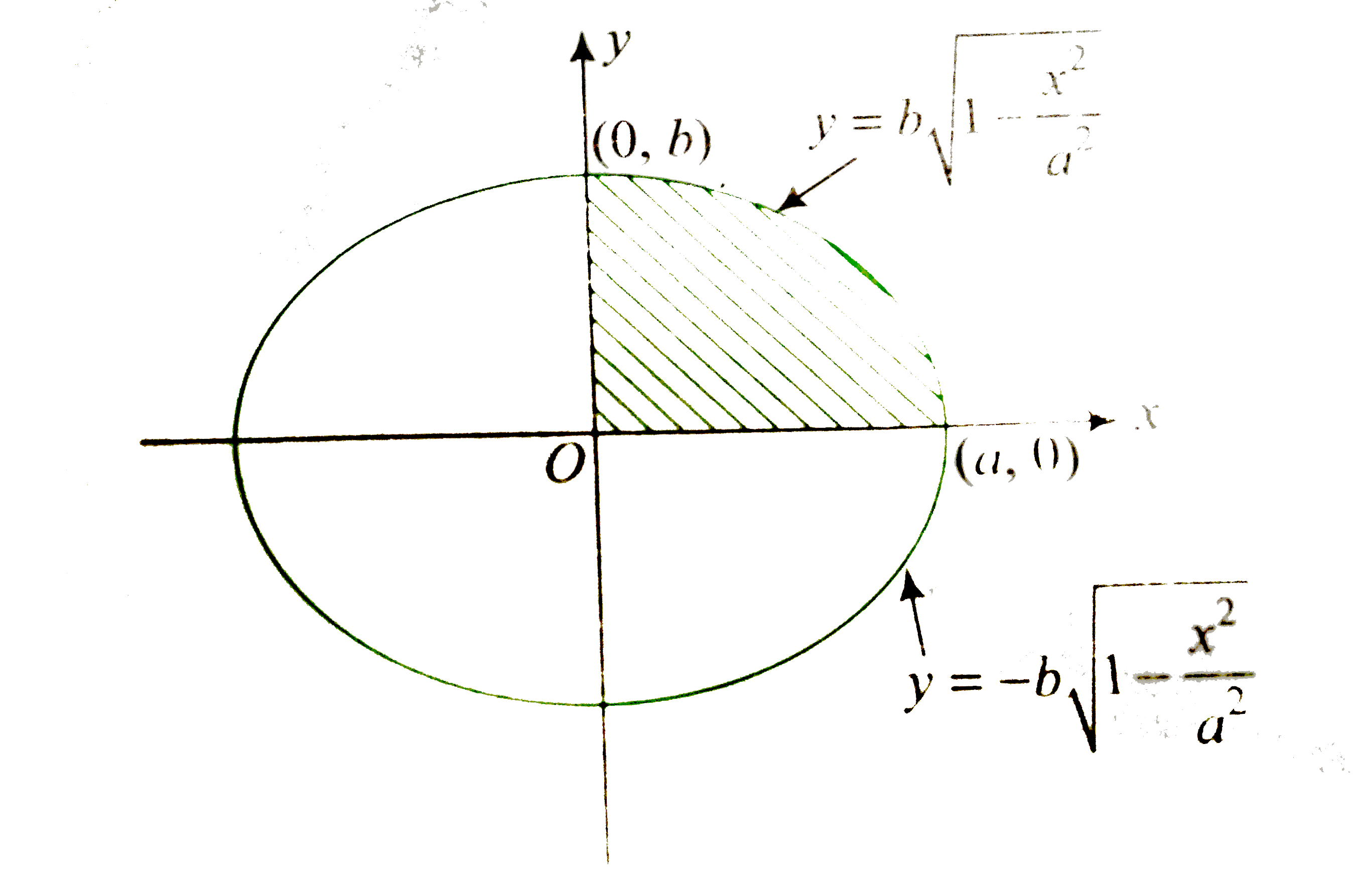
Since graph of the ellipse x2a2+y2b2=1 is symmetrical about both the axis,
Area enclosed by ellipse =4× Area in the first quadrant
=4×a∫0b√−1x2a2dx
=4baa∫0√a2−x2dx
=4ba[x2√a2−x2+a22sin−1xa]a0
=4ba[0+a22sin−11−0−0]
=4b2[a22⋅π2]
=πab
In the following figure ellipse and its auxiliary are drawn.
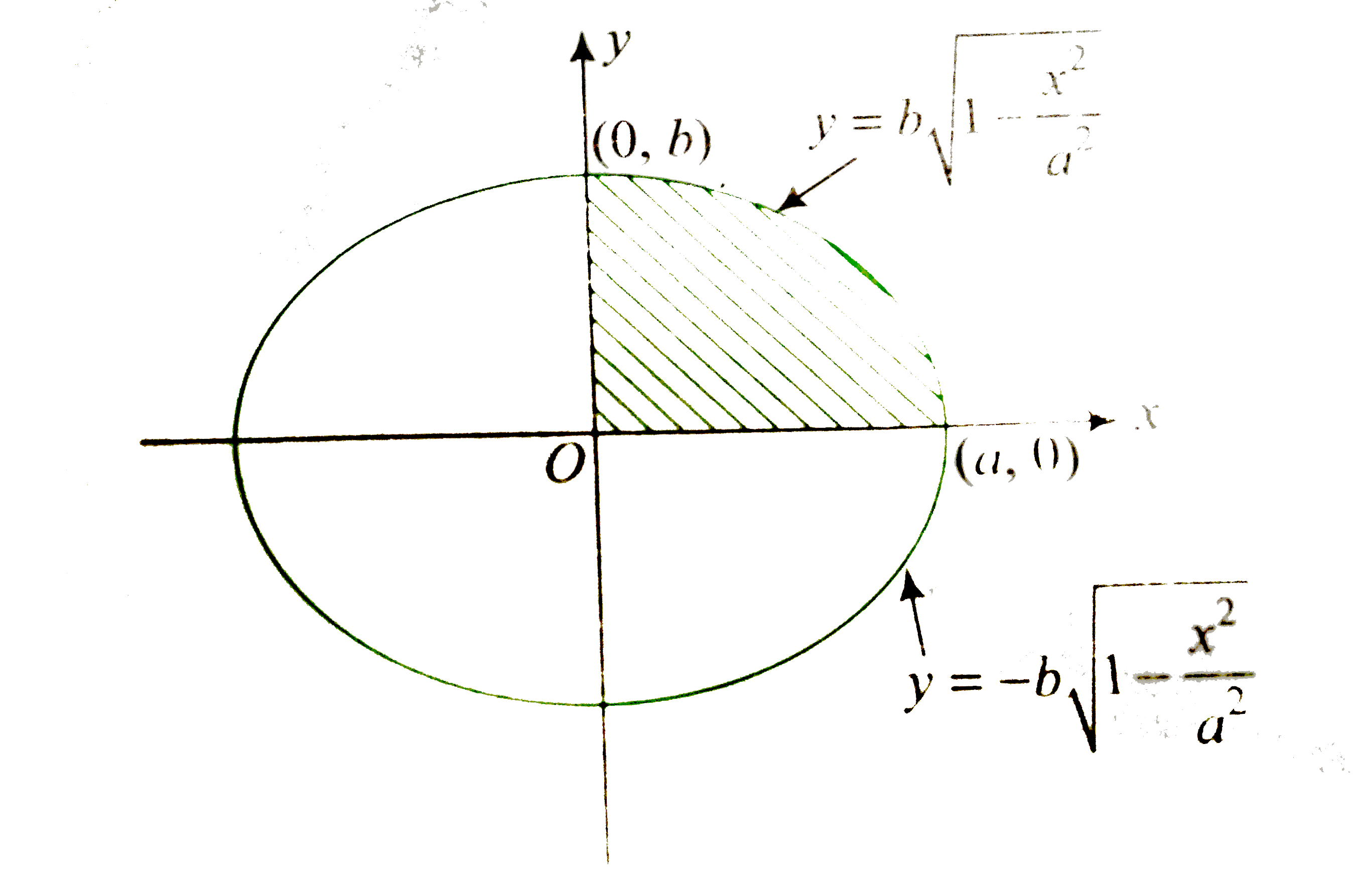 ltbvrgt Area of the ellipse =πab
ltbvrgt Area of the ellipse =πab
Area of the circle =πa2
Common area between curves is that shown as shaded region
=Area of circle - area of ellipse
=πab−πa2
=πa(b−a)
This is area of the ellipse whose semi axis are a and (a-b).
One of the possible equations of ellipse is x22+y2(a−b)2=1
Topper's Solved these Questions
- AREABOOK - CENGAGE PUBLICATIONCHAPTER - AREAEXERCISE - Solved Examples
10 Videos
- AREABOOK - CENGAGE PUBLICATIONCHAPTER - AREAEXERCISE - Concept Application Exercise 9.1
9 Videos
- APPLICATIONS OF DERIVATIVESBOOK - CENGAGE PUBLICATIONCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Subjective Type
2 Videos
- BINOMIAL THEOREMBOOK - CENGAGE PUBLICATIONCHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension
11 Videos
Similar Questions
Find the area bounded by the curve x2=y,x2=−yandy2=4x−3
View SolutionFind the area of the smaller part of the circle x2+y2=a2 cut off by the line x=a√2.
View SolutionProve that for λ>1, the equation xlogx+x=λ has least one solution in [1,λ].
View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is
View SolutionProve that area common to ellipse x2a2+y2b2=1 and its auxiliary circle x2+y2=a2 is equal to the area of another ellipse of semi-axis aanda−b.
View SolutionProve that the area bounded by the circle x2+y2=a2 and the ellipse x2a2+y2b2=1 is equal to the area of another ellipse having semi-axis a−b and b,a>b .
View SolutionThe ellipse x2a2+y2b2=1 is such that its has the least area but contains the circel (x−1)2+y2=1
The equation of the auxiliary circle of ellipse is
View SolutionThe area of the ellipse (x^(2))/(a^(2))+(y^(2))/(b^(2))=1 is
View Solutionदीर्घवृत्त x2a2+y2b2=1 का क्षेत्रफल -
View SolutionIf the area of the auxiliary circle of the ellipse x2a2+y2b2=1(a>b) is twice the area of the ellipse, then the eccentricity of the ellipse is
View SolutionIf the area of the auxillary circle of the ellipse x2a2+y2b2=1(a>b) is twice the area of the ellipse, then the eccentricity of the ellipse is
View SolutionIf the area of the auxilliary circle of the ellipse x2a2+y2b2=1(a>b) is twice the area of the ellipse, then the eccentricity of the ellipse is
View SolutionEllipse (x^(2))/(a^(2))+(y^(2))/(b^(2))=1 This is such that its area is the lowest but the circle (x-1)^(2)+y^(2)=1 Contains The equation of the auxiliary circle of the ellipse is
View SolutionProve that the area bounded by the circle x2+y2=a2 and the ellipse x2a2+y2b2=1 is equal to the area of another ellipse having semi-axis a−b and b,a>b .
View SolutionProve that area common to ellipse x2a2+y2b2=1 and its auxiliary circle x2+y2=a2 is equal to the area of another ellipse of semi-axis a and a-b.
View SolutionThe area of the ellipse (x^(2))/(a^(2))+(y^(2))/(b^(2))=1 is
View Solution
