Let f(x)=f1(x)−2f2(x), where ,where f1(x)={(min{x2,|x|}|x|≤1max{x2,|x|}|x|≤1) and f2(x)={(min{x2,|x|}|x|<1{x2,|x|}|x|≤1) and let g(x)={(min{f(t):−3≤t≤x,−3≤x≤0}max{f(t):0≤t≤x,0≤x≤3}) for −3≤x≤−1 the range of g(x) is Solution in Bengali
[−1,3]
[−1,−15]
[−1,9]
None of these
The correct Answer is:A
f1(x)=x2andf2(x)=|x|
orf(x)=f1(x)−2f2(x)=x2−2|x|
Graph of f(x)
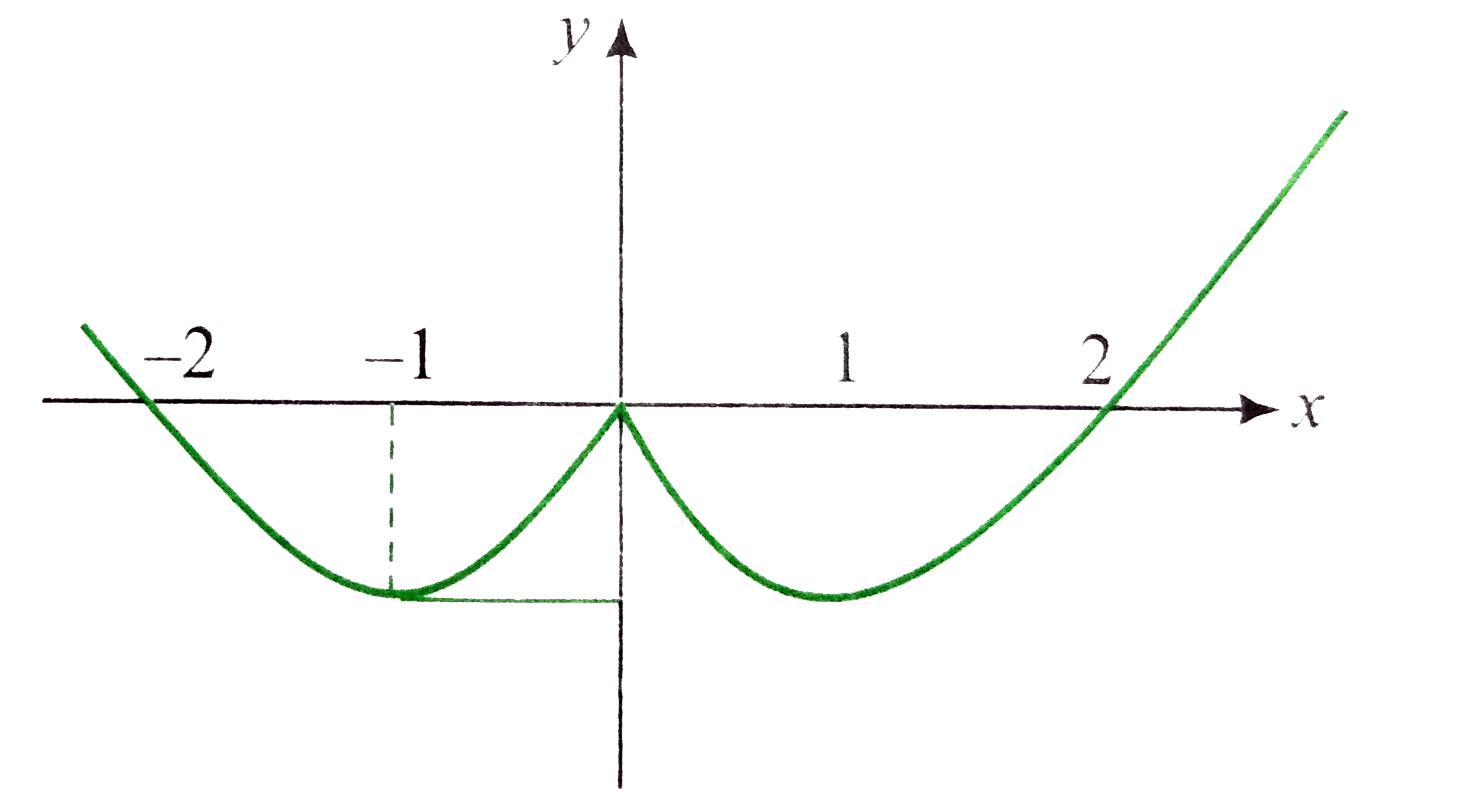
g(x)=⎧⎪
⎪
⎪
⎪⎨⎪
⎪
⎪
⎪⎩f(x),−3≤x<−1−1,−1≤x<00,0≤x≤2f(x),2<x≤3=⎧⎪
⎪
⎪
⎪⎨⎪
⎪
⎪
⎪⎩x2+2x,−3≤x<−1−1,−1≤x<00,0≤x≤2x2−2x,2<x≤3
The range of g(x) for [-3, -1] is [-1, 3].
Topper's Solved these Questions
Similar Questions
Let ABCandABC' be two non-congruent triangles with sides AB=4,AC=AC′=2√2 and angle B=300 . The absolute value of the difference between the areas of these triangles is
View SolutionNumber of integral value(s) of λ for which vectors x2ˆi−ˆj+xˆk,(λ−1)ˆi−2λˆj−ˆk and ˆi−ˆj+ˆk, in the order form right-handed system ∀x ∈R, is
(a) 0 (b) 2 (c) 4 (d) 6
View SolutionLet f(x)=f_1(x)-2f_2 (x), where ,where f_1(x)={((min{x^2,|x|},|x|le 1),(max{x^2,|x|},|x| le 1)) and f_2(x)={((min{x^2,|x|},|x| lt 1),({x^2,|x|},|x| le 1)) and let g(x)={ ((min{f(t):-3letlex,-3 le x le 0}),(max{f(t):0 le t le x,0 le x le 3})) for -3 le x le -1 the range of g(x) is
View SolutionLet f(x)=f1(x)−2f2(x), where
where f(x)={min{x2,|x|},|x|≤1max{x2,|x|},|x|>1
and f2(x)={min{x2,|x|},|x|>1max{x2,|x|},|x|≤1
and let g(x)={min{f(t):−3≤t≤x, −3≤x<0}max{f(t):0≤t≤x, 0≤x≤3}
For x∈(−1,0),f(x)+g(x) is
View SolutionLet f(x) and g(x) be two functions given by f(x)=−1|x−1|,−1≤x≤3 and g(x)=2−|x+1|,−2≤x≤2
Then,
View SolutionLet f(x)=x3−x2+x+1andg(x) be a function defined by g(x)={Max{f(t):0≤t≤x}0≤x≤13−x1≤x≤2 Then, g(x) is
View SolutionLet f(x)=x3−x2+x+1andg(x)={maxf(t),0≤t≤xfor0≤x≤13−x,1<x≤2 Then, g(x) in [0, 2] is
View SolutionLet f(x)=−x3+x2−x+1andg(x)={min(f(t)),0≤t≤xand0≤x≤1x−1,1<x≤2 Then, the value of limx→1g(g(x)), is........ .
View Solutionमाना f(x)=x3−x2+x+1 और g(x)={max{f(t),0≤t≤x}0≤x≤13−x1<x≤2
फलन g(x) की सततता तथा अवकलनीयता अंतराल (0, 2) पर ज्ञात कीजिए |
View SolutionLet f(x)=f1(x)−2f2(x), where ,where f1(x)={(min{x2,|x|}|x|≤1max{x2,|x|}|x|≤1) and f2(x)={(min{x2,|x|}|x|<1{x2,|x|}|x|≤1) and let g(x)={(min{f(t):−3≤t≤x,−3≤x≤0}max{f(t):0≤t≤x,0≤x≤3}) for −3≤x≤−1 the range of g(x) is
View SolutionLet f(x)=x3−x2+x+1 g(x) = max I {f(t),0≤t≤x},0≤x≤1=3−x,1<x≤2
Then in [0, 2] the points where g(x) is not differentiable is………
View SolutionLet f(x)=x3−x2+x+1 g(x)={max(f(t)),0≤t≤x},0≤x≤1}{3−x,1<x≤2}
Then in [0, 2] the points where g(x) is not differentiable is………
View SolutionLet f(x)=f1(x)−2f2(x), where where
f1(x)={min{x2,|x|}|x|≤1min{x2,|x|}|x|>1
and f2(x)={min{x2,|x|}|x|>1min{x2,|x|}|x|≤1and let g(x)={min{f(t):−3t≤x,−3≤x<0}min{f(t):0≤t≤x,0≤x≤3}
For −3≤x≤−1 the range of g(x) is
View SolutionLet f(x)=f1(x)−2f2(x), where where
f1(x)={min{x2,|x|}|x|≤1min{x2,|x|}|x|>1
and f2(x)={min{x2,|x|}|x|>1min{x2,|x|}|x|≤1and let g(x)={min{f(t):−3t≤x,−3≤x<0}min{f(t):0≤t≤x,0≤x≤3}
For x∈(−1,0),f(x)+g(x) is
View SolutionLet f(x)=f1(x)−2f2(x), where where
f1(x)={min{x2,|x|}|x|≤1min{x2,|x|}|x|>1
and f2(x)={min{x2,|x|}|x|>1min{x2,|x|}|x|≤1and let g(x)={min{f(t):−3t≤x,−3≤x<0}min{f(t):0≤t≤x,0≤x≤3}
The graph of y = g(x) in its doman is broken at
View SolutionLet f(x)=x3−x2+x+1andg(x)={maxf(t),0≤t≤xfor0≤x≤13−x,1<x≤2 Then, g(x) in [0, 2] is
View Solution