Number of solutions of the equation, [y+[y]]=2cosx is: (where y=(1/3)[sinx+[sinx+[sinx]]] and []= greatest integer function) 0 (b) 1 (c) 2 (d) ∞Solution in Bengali
4
2
3
0
The correct Answer is:D
[y+[y]]=2cosx
or[y]+[y]=2cosx (∵[x+n]=[x]+n if n∈I)
or2[y]=2cosxor[y]=cosx (1)
Also, y=13[sinx+[sinx+[sinx]]]
=13(3[sinx])
=[sinx] (2)
From (1) and (2),
[[sinx]]=cosx
or[sinx]=cosx
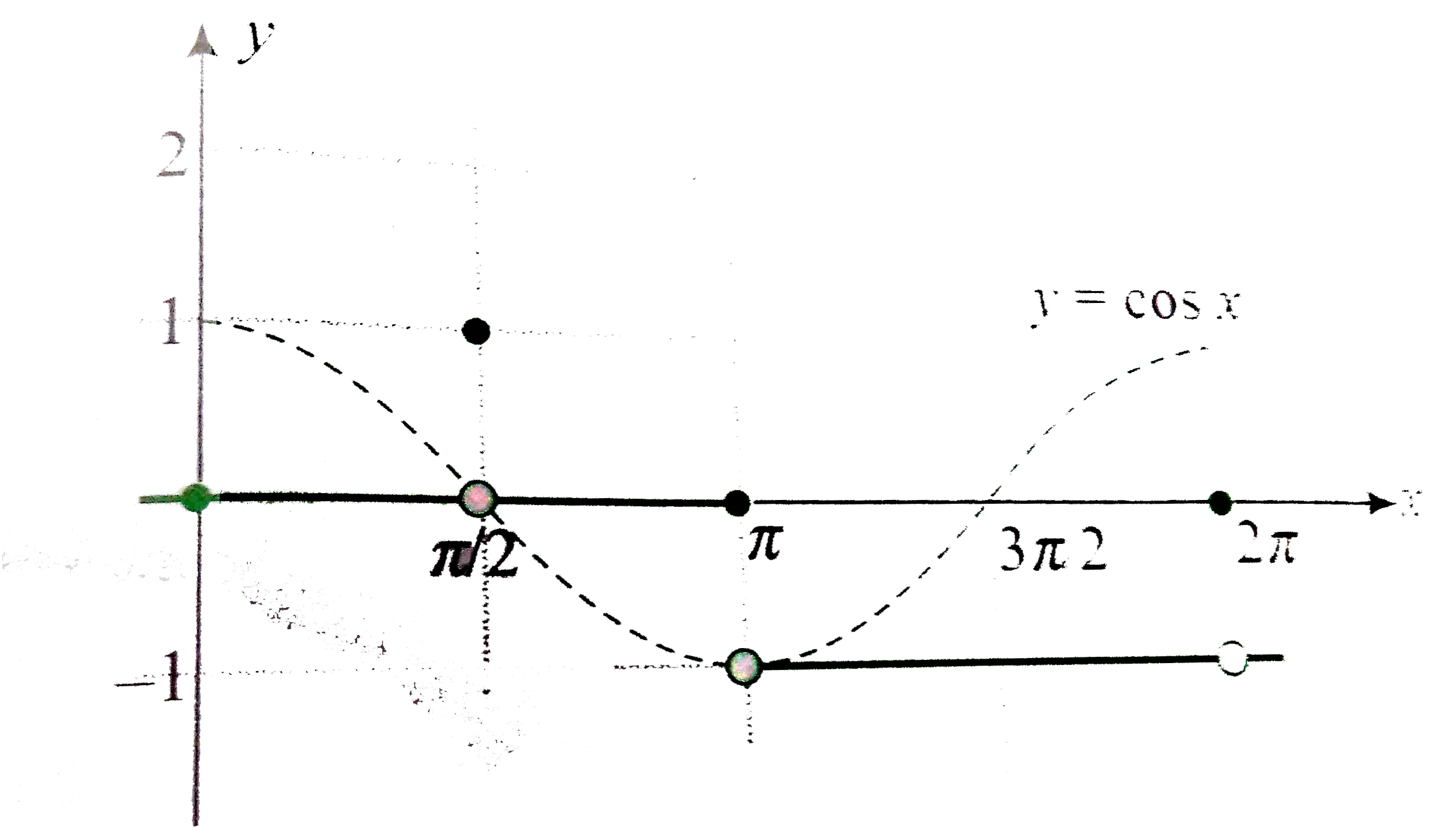
The number of solutions is 0.
Topper's Solved these Questions
Similar Questions
Let ABCandABC' be two non-congruent triangles with sides AB=4,AC=AC′=2√2 and angle B=300 . The absolute value of the difference between the areas of these triangles is
01:30View SolutionNumber of integral value(s) of λ for which vectors x2ˆi−ˆj+xˆk,(λ−1)ˆi−2λˆj−ˆk and ˆi−ˆj+ˆk, in the order form right-handed system ∀x ∈R, is
(a) 0 (b) 2 (c) 4 (d) 605:09View SolutionThe number of solutions of the equation |cosx−sinx|=2cosx∈[0,2π] is (A) 1 (B) 2 (C) 3 (D) 4
03:41View SolutionIf [.] represents greatest integer function then find the number of solution in the equation sinx=[1+sinx]+[1-cosx] in [0,2pi]
03:17View SolutionThe number of solutions of the equation [y+[y]]=2cosx, where y=13[sinx+[sinx+[sinx]]] (where [.] denotes the greatest integer function) is
05:23View SolutionIf y=(sinx)(sinx)(sinx)...∞, prove that dydx=y2cotx(1−ylogsinx).
01:45View SolutionIf y=(sinx)(sinx)(sinx)....∞show that,
dydx=y2cotx1−ylog(sinx)03:41View SolutionNumber of solutions of the equation, [y+[y]]=2cosx is: (where y=1/3)[sinx+[sinx+[sinx]]] and []= greatest integer function) 0 (b) 1 (c) 2 (d) ∞
View SolutionIf y=(sinx)(sinx)(sinx)...∞ , prove that dydx=y2cosx(1−ylogsinx)
View SolutionIf [y]=sinx(x) and y=cosx are two given equations then the number of solutions is (where [.] denotes the greatest integer function)
04:32View Solutionसमीकरण [y+[y]]=2cosx के हलो की संख्या है-
(जहाँ y=(1/3)[sinx+[sinx]]] और []= महत्तम पूर्णाक फलन है।)03:38View SolutionNumber of solution of equation y=13[sinx+[sinx+[sinx]]] and [y+[y]]=2cosx is/are
01:21View SolutionNumber of solutions of the equation, [y+[y]]=2cosx is: (where y=1/3)[sinx+[sinx+[sinx]]] and []= greatest integer function) (a). 0 (b) 1 (c) 2 (d) ∞
01:17View SolutionThe number of solutions of the equation |cosx−sinx|=2cosx∈[0,2π] is (A) 1 (B) 2 (C) 3 (D) 4
05:01View SolutionNumber of solutions of the equation, [y+[y]]=2cosx is: (where y=1/3)[sinx+[sinx+[sinx]]] and []= greatest integer function) 0 (b) 1 (c) 2 (d) ∞
02:43View SolutionThe number of solutions of the equation [y+[y]]=2cosx, where y=13[sinx+[sinx+[sinx]]] (where [.] denotes the greatest integer function) is
05:44View Solution
