Identify the following functions : f(x)=xg(x)g(−x)+tan(sinx)Solution in Bengali
Odd
Even
Neither
Both
The correct Answer is:A
f(−x)=(−x)g(−x)⋅g(x)+tan(sin(−x))
=−(xg(x)g(−x)+tan(sinx))=−f(x)
Hence, f(x) is an odd function.
Topper's Solved these Questions
Similar Questions
Let ABCandABC' be two non-congruent triangles with sides AB=4,AC=AC′=2√2 and angle B=300 . The absolute value of the difference between the areas of these triangles is
View SolutionNumber of integral value(s) of λ for which vectors x2ˆi−ˆj+xˆk,(λ−1)ˆi−2λˆj−ˆk and ˆi−ˆj+ˆk, in the order form right-handed system ∀x ∈R, is
(a) 0 (b) 2 (c) 4 (d) 6
View SolutionIdentify the following functions whether odd or even or neither: f(x)=xg(x)g(−x)+tan(sinx)
View SolutionIf ∫sinxd(secx)=f(x)−g(x)+c,then f(x)=secx (b) f(x)=tanx g(x)=2x (d) g(x)=x
View SolutionLet f and g be two differential functions such that f(x)=g'(1)sin x+(g''(2)-1)xg(x)=x^(2)-f'((pi)/(2))x+f''((-pi)/(2))
View Solutionf(x)=x2+xg'(1)+g''(2)andg(x)=f(1)x2+xf'(x)+f'(x).
The domain of the function √f(x)g(x) is
View SolutionIf g is inverse of function f and f'(x)=sinx, then g'(x)=
View SolutionIf limx→af(x)=1 and limx→ag(x)=∞ then limx→a{f(x)}g(x)=elimx→a(f(x)−1)xg(x)
limx→0(sinxx)sinxx−sinx is equal to
View Solutionf(x)=x2+xg'(1)+g''(2) and g(x)=f(1)x2+xg'(1)+f''(x).
The domain of the function √f(x)g(x) is-
View SolutionIf f:R→Randg:R→R are two functions such that f(x)+f''(x)=−xg(x)f'(x)andg(x)>0∀x∈R then the function f2(x)+(f'(x))2 has
View SolutionIdentify the following functions whether odd or even or neither: f(x)=xg(x)g(−x)+tan(sinx)
View Solutionf(x)=x2+xg'(1)+g''(2)andg(x)=f(1)x2+xf'(x)+f'(x).
The domain of the function √f(x)g(x) is
View SolutionIdentify the following functions : f(x)=xg(x)g(−x)+tan(sinx)
View SolutionIf f(x)=sin(sinx)anff'(x)+tanxf'(x)+g(x)=0, then g(x) is :
View Solutionf(x)=x2+xg'(1)+g''(2)andg(x)=f(1)x2+xf'(x)+f''(x)
The domain of the function √f(x)g(x) is
View SolutionConsider the graph of the function f(x)(a)Identify the function f(x)……..(iii)f(x)=tanx
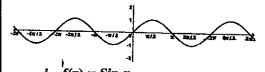
View Solution