Solve sinx≻12or find the domain of f(x)=1√1+2sinxSolution in Bengali
To define f(x), we must have 1+2sinx>0orsinx>−12.
The function sinx has the least positive period 2π. That is why it is sufficient to solve the inequalities of the form sinx>a,sinx≥a,sinx<a,andx≤a first on the interval of length 2π, and then get the solution set by adding numbers of the form 2πn,n∈Z, to each of the solutions obtained on that interval.
Thus, let us solve this inequality on the interval [−π2,3π2].
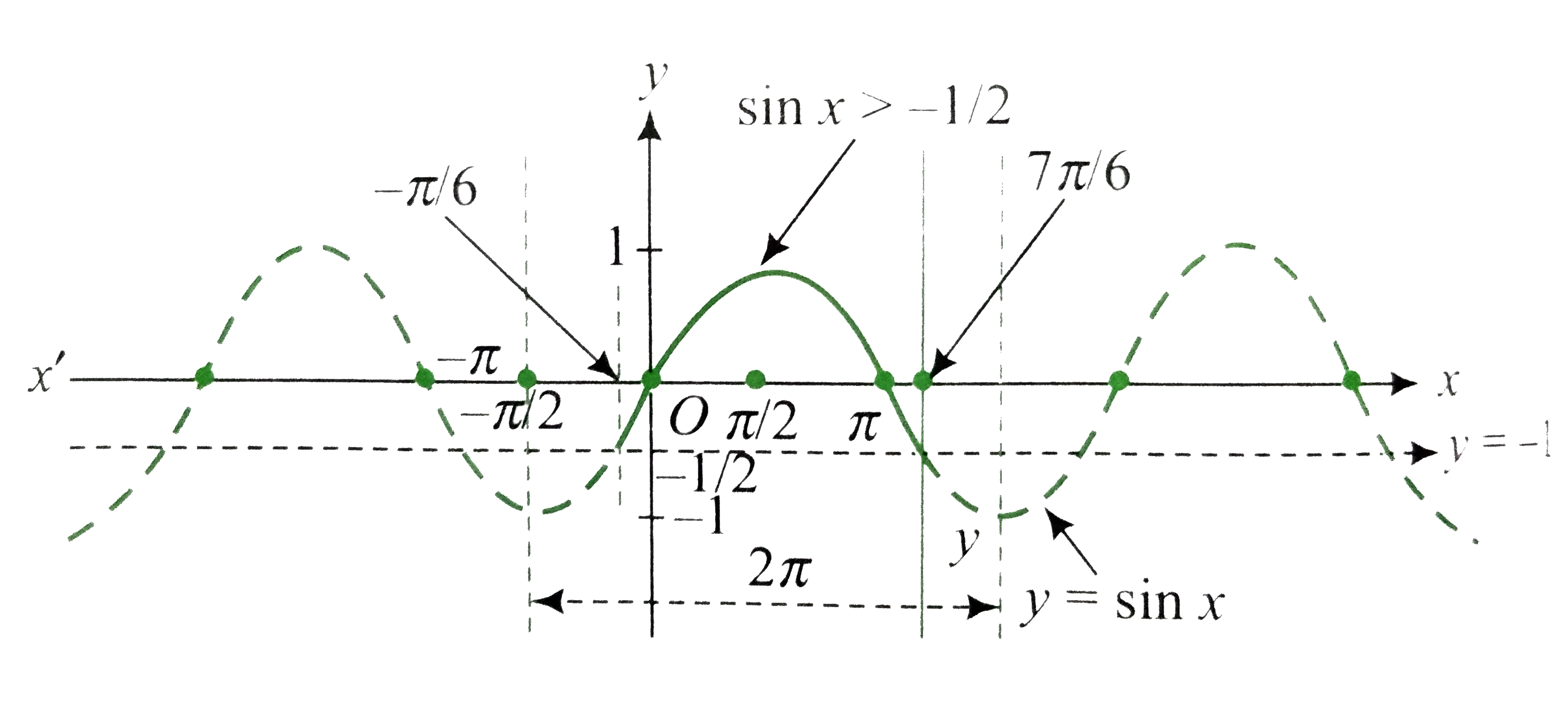
From the figure,
sinx>−12 when −π6<x<7π6
Thus, on generalizing the above solution, we get
x∈∪n∈z(−π6+2nπ,7π6+2nπ)
Topper's Solved these Questions
Similar Questions
Let ABCandABC' be two non-congruent triangles with sides AB=4,AC=AC′=2√2 and angle B=300 . The absolute value of the difference between the areas of these triangles is
View SolutionNumber of integral value(s) of λ for which vectors x2ˆi−ˆj+xˆk,(λ−1)ˆi−2λˆj−ˆk and ˆi−ˆj+ˆk, in the order form right-handed system ∀x ∈R, is
(a) 0 (b) 2 (c) 4 (d) 6
View SolutionSolve sinx≻12or find the domain of f(x)=1√1+2sinx
View SolutionFind the domain of 11−2sinx.
View SolutionFind the domain of f(x)=11−2sinx
View SolutionIf f(x) =sqrt(4-x^(2)) +1/(sqrt(abs(sinx)-sinx)) , then the-domain of f(x) is
View SolutionThe domain of f(x)=√(1sinx−1) is :
View SolutionThe domain of f(x)= ⎷log(1|sinx|) is :
View SolutionFind the domain of the function f(x)=11+2sinx
View SolutionSolve sinx > −12 or find the domain of f(x)=1√1+2sinx
View SolutionFind the domain of the function f(x)=11+2sinx
View SolutionSolve sinx≻12or find the domain of f(x)=1√1+2sinx
View SolutionFind the domain of each of the following functions:
f(x)=√sinx−1
View SolutionLet f(x)=√sinx1+(sinx)13 then domain f contains
View SolutionFind the domain of the function f(x)=11+2sinx
View SolutionSolve sinx≻12or find the domain of f(x)=1√1+2sinx
View Solution