Solve |x−1|+|x−2|≥4Solution in Bengali
Video Solution
Text Solution
Let f(x)=|x−1|+|x−2|
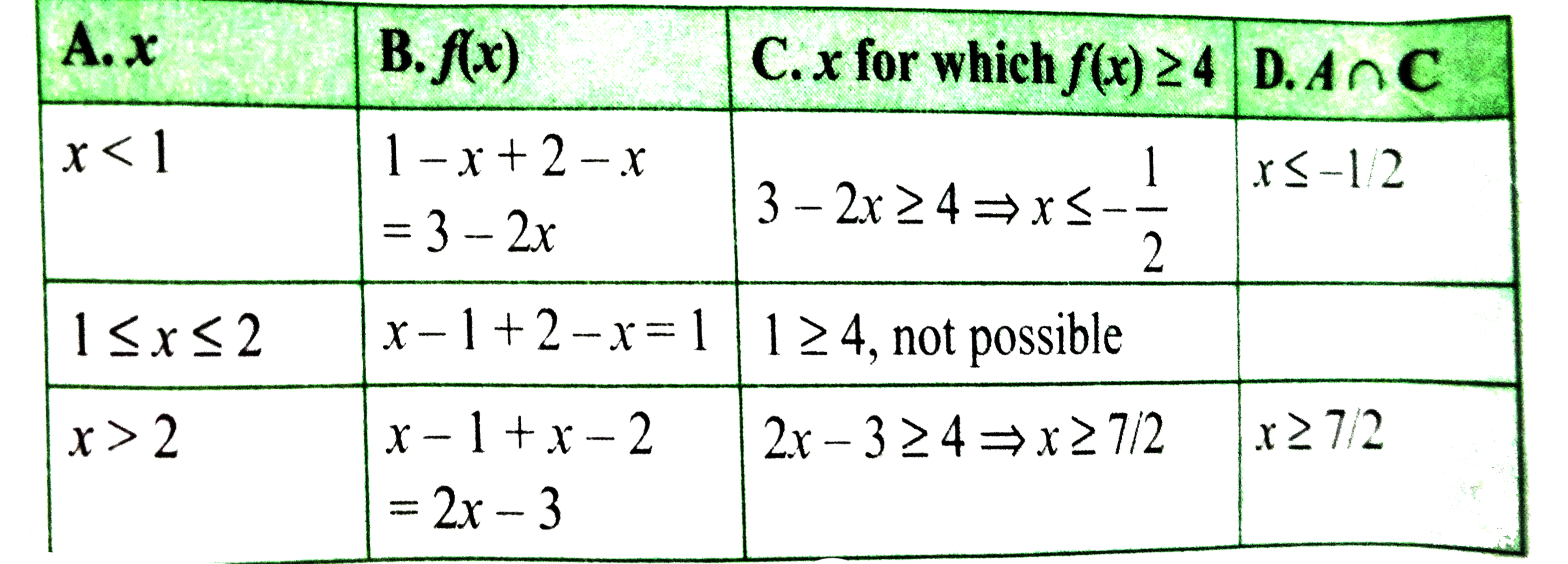
Hence, solutions is x∈(−∞,−1/2]∪[7/2,∞).
Alternative Method:
Consider |x−1|+|x−2|<4
Now, |(x−1)+(x−2)|≤|x−1|+|x−2|
∴|(x−1)|+(x−2)∣<4
⇒|2x−3|<4
⇒−4<2x−3<4
⇒−1<2x<7
⇒−1/2<x<7/2
Therefore, for |x−1|+|x−2|≥4, we have
x∈(−∞,−1/2]∪[7/2,∞).
|
Updated on:21/07/2023
Related Playlists
Similar Questions
Let ABCandABC' be two non-congruent triangles with sides AB=4,AC=AC′=2√2 and angle B=300 . The absolute value of the difference between the areas of these triangles is
04:15View SolutionNumber of integral value(s) of λ for which vectors x2ˆi−ˆj+xˆk,(λ−1)ˆi−2λˆj−ˆk and ˆi−ˆj+ˆk, in the order form right-handed system ∀x ∈R, is
(a) 0 (b) 2 (c) 4 (d) 601:40View Solutionsolve: |x−2|+|x−4|≥8
04:04View Solutionsolve : 3x−42+1≥x+14
03:18View SolutionSolve : |x−1|+|x−2|≥3
03:38View SolutionSolve |x−1|+|x−2|≥4
00:58View SolutionSolve : |x|−|x−2|≥1
02:16View Solutionहल कीजिए 3x−42+1≥x+14
05:20View Solutionहल कीजिए |x−1|+|x−2|≥3
01:09View Solutionहल कीजिए
|x−1|+|x−2|≥403:46View SolutionSolve the inequality 3x−42≥x+14−1.
04:28View SolutionSolve |x−1|+|x−2|≥4
04:12View SolutionSolve |x−1|+|x−2|≥4
08:12View SolutionSolve |x−1|+|x−2|≥4
04:10View SolutionSolve : |x|−|x−2|≥1
01:30View Solutionsolve: |x−2|+|x−4|≥8
03:58View Solution


