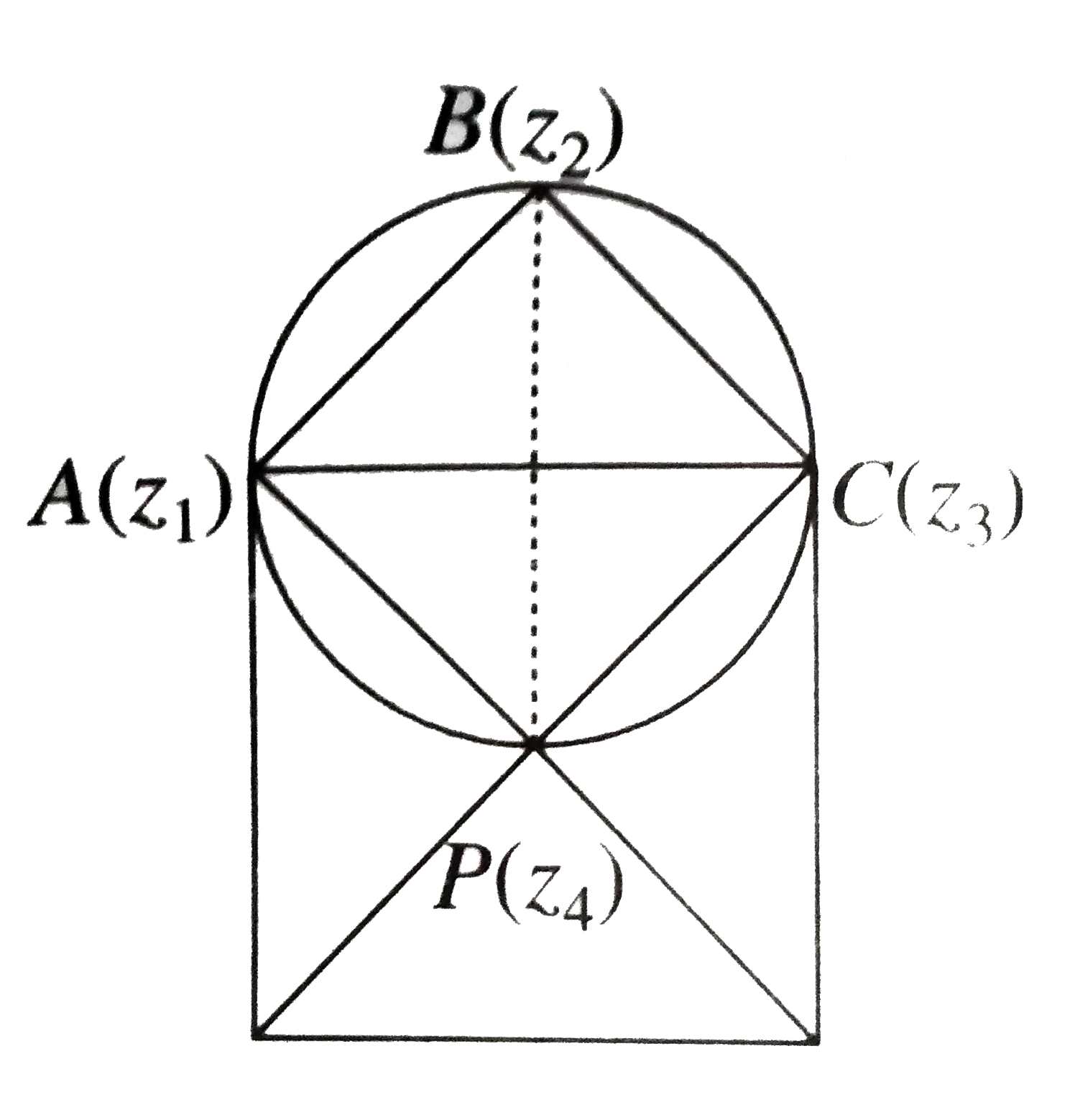
Let z1, z2, z3 are the vertices of ΔABC, respectively, such that z3−z2z1−z2 is purely imaginery number. A square on side AC is drawn outwardly. P(z4) is the centre of square, thenSolution in Bengali
|z1−z2|=|z2−z4|
arg(z1−z2z4−z2)+arg(z3−z2z4−z2)=+π2
arg(z1−z2z4−z2)+arg(z3−z2z4−z2)=0
z1, z2, z3 and z4 lie on a circle
The correct Answer is:C, D
(c,d) P is centre of square ⇒AP=PC and ∠APC=π2
∠ABC is also π2.
⇒ABCP is cyclic quadrilateral
⇒A,B,C,P lie on a circle.
⇒ In circl chord, AP=PC
⇒ arc AP= are PC
⇒∠ABP=∠PBC
⇒BP is angular bisector.
Let arg(z1−z2z4−z2)=−α........(i)
⇒arg(z3−z2z4−z2)=α..........(ii)
Add (i) and (ii), arg(z1+z2z4−z2)+arg(z3−z2z4−z2)=0
Topper's Solved these Questions
- COMPLEX NUMBERSBOOK - CENGAGE PUBLICATIONCHAPTER - COMPLEX NUMBERSEXERCISE - Matching Column
1 Videos
- COMPLEX NUMBERSBOOK - CENGAGE PUBLICATIONCHAPTER - COMPLEX NUMBERSEXERCISE - Comprehension
11 Videos
- COMPLEX NUMBERSBOOK - CENGAGE PUBLICATIONCHAPTER - COMPLEX NUMBERSEXERCISE - MULTIPLE CORRECT ANSWER TYPE
6 Videos
- CIRCLESBOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLESEXERCISE - Comprehension Type
8 Videos
- CONIC SECTIONSBOOK - CENGAGE PUBLICATIONCHAPTER - CONIC SECTIONSEXERCISE - All Questions
102 Videos
Similar Questions
Evaluate :
i−47
View SolutionConsider the region R in the Argand plane described by the complex number. Z satisfying the inequalities |Z−2|≤|Z−4|, |Z−3|≤|Z+3|, |Z−i|≤|Z−3i|, |Z+i|≤|Z+3i|
Answer the followin questions :
Maximum of |Z1−Z2| given that Z1, Z2 are any two complex numbers lying in the region R is
View SolutionLet z1 and z2 be two distinct complex numbers and z=(1−t)z1+tz2, for some real number t with 0<t<1 and i=√−1. If arg(w) denotes the principal argument of a non-zero compolex number w, then
View Solution
In the diagram as shown, a circle is drawn with centre C(1,1) and radius 1 and a line L. The line L is tangent to the circle at Q. Further L meets the y-axis at R and the x-axis at P in such a way that the angle OPQ equals θ where 0<θ<π2.
Coordinate of Q is
View SolutionGiven that A(1,1) and B(2,−3) are two points and D is a point on AB produced such that AD=3AB. Find the coordinates of D.
View SolutionLet z_(1),z_(2),z_(3) be three distinct complex numbers satisfying |z_(1)-1|=|z_(2)-1|=|z_(3)-1|* If z_(1)+z_(2)+z_(3)=3 then z_(1),z_(2),z_(3) must represent the vertices of
View SolutionThe vertices of a square are z_(1),z_(2),z_(3) and z_(4) taken in the anticlockwise order,then z_(3)=
View SolutionLet A(z1),B(z2),C(z3 and D(z4) be the vertices of a trepezium in an Argand plane such that AB∣∣CD Let |z1−z2|=4,|z3,z4|=10 and the diagonals AC and BD intersects at P. It is given that Arg(z4−z2z3−z1)=π2 and Arg(z3−z2z4−z1)=π4
Which of the following option(s) is/are correct?
View SolutionLet A(z1),B(z2),C(z3 and D(z4) be the vertices of a trepezium in an Argand plane such that AB∣∣CD Let |z1−z2|=4,|z3,z4|=10 and the diagonals AC and BD intersects at P. It is given that Arg(z4−z2z3−z1)=π2 and Arg(z3−z2z4−z1)=π4
Which of the following option(s) is/are incorrect?
View SolutionLet z1, z2, z3 are the vertices of ΔABC, respectively, such that z3−z2z1−z2 is purely imaginery number. A square on side AC is drawn outwardly. P(z4) is the centre of square, then
View SolutionIf |z1|=|z2|=|z3| and z1+z2+z3=0, then z1,z2,z3 are vertices of
View SolutionComplex numbers z1,z2,z3 are the vertices of A,B,C respectively of an equilteral triangle. Show that z21+z22+z23=z1z2+z2z3+z3z1.
View SolutionIf z1,z2,andz3 are three complex numbers such that |z1|=1, |z2|=2, |z3|=3and|z1+z2+z3|=1, show that |9z1z2+4z1z3+z2z3|=6.
View SolutionIf z1,z2,z3 are collinear and z3−z1z2−z1 is purely real, then arg(z3−z1z2−z1)
View SolutionIf z1,z2,z3 are collinear and z3−z1z2−z1 is purely real, then arg(z3−z1z2−z1)
View Solution
