Let f(x)=log(log)13((log)7(sinx+a))) be defined for every real value of x, then the possible value of a is 3 (b) 4 (c) 5 (d) 6Solution in Bengali
3
4
5
6
The correct Answer is:A, B, C
log1/3log6(sinx+a)>0
or0<log7(sinx=a)<1
or1<(sinx+a)<7,∀x∈R
or1−six<a<7−sinx
It is found that a should by less thanthe minimum value of (7 - sinx) and a must be greater the the maximum value of (1 - sinx). Thus,
⇒2<a<6
Topper's Solved these Questions
- TRIGONOMETRIC FUNCTIONS BOOK - CENGAGE PUBLICATIONCHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - Linked Comprehension Type
11 Videos
- TRIGONOMETRIC FUNCTIONS BOOK - CENGAGE PUBLICATIONCHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - Matrix Match Type
3 Videos
- TRIGONOMETRIC FUNCTIONS BOOK - CENGAGE PUBLICATIONCHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - Exercises
57 Videos
- TRIGONOMETRIC EQUATIONSBOOK - CENGAGE PUBLICATIONCHAPTER - TRIGONOMETRIC EQUATIONSEXERCISE - Archives (Numerical value type)
4 Videos
- TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULASBOOK - CENGAGE PUBLICATIONCHAPTER - TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULASEXERCISE - Archives (Numerical Value Type)
2 Videos
Similar Questions
Let us consider the equation cos^4x/a xa+sin4xb=1a+b,x∈[0,π2],a,b>0 the value of sin8xb3+cos8xa3 is
View Solution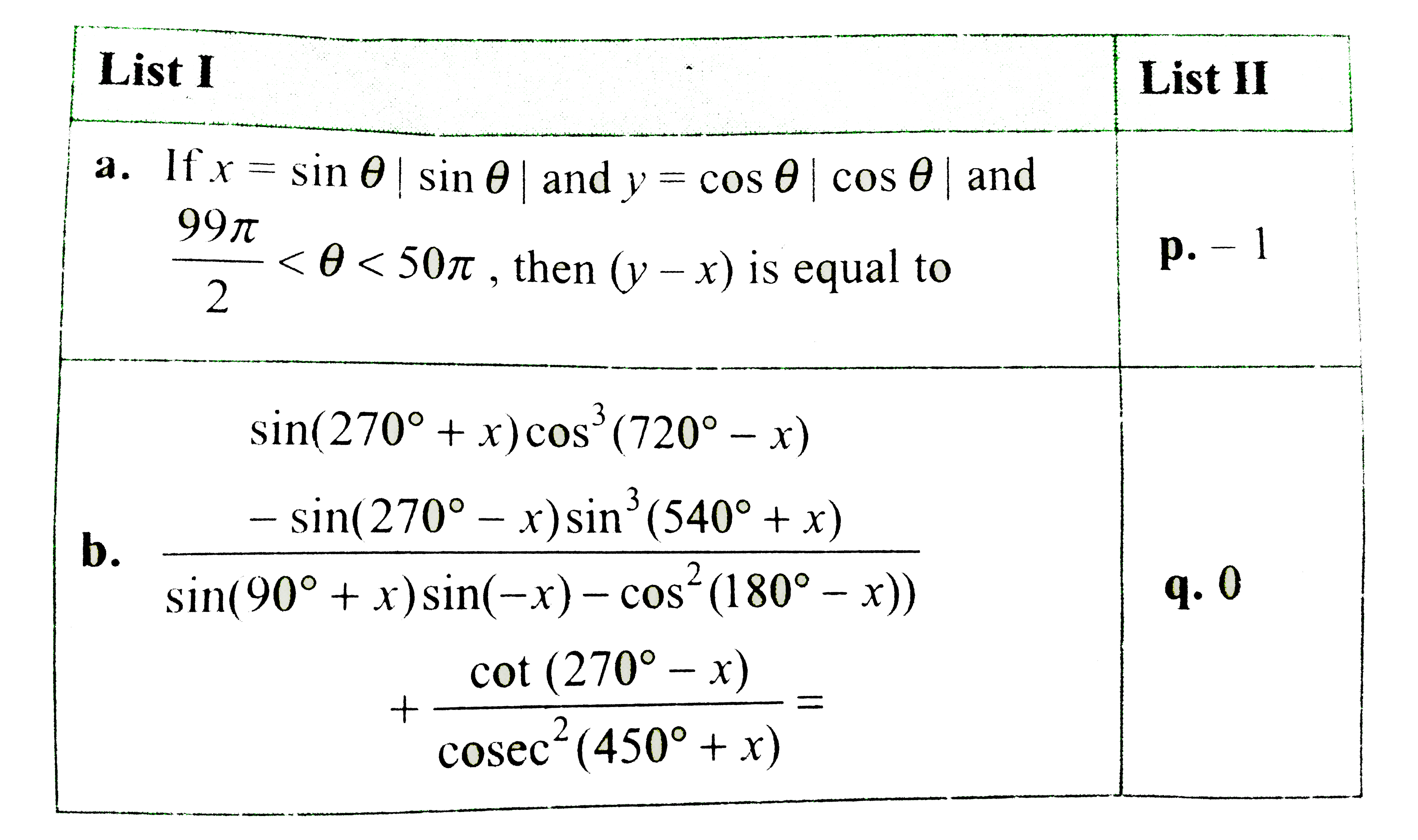
View SolutionIf tanθ=3, then sinθ−cosθsinθ+cosθ is equal to
View SolutionThe number of all possible values of θ, where 0<θ<π, for which the system of equations (y+z)cos3θ=(xyz)sin3θ,xsin3θ=2cos3θy+2sin3θzand(xyz)sin3θ=(y+2z)cos3θ+ysin3θ have a solution (x0,y0,z0) wiith y0z0≠0 is
View SolutionThe maximum value of the expression 1sin2θ+3sinθcosθ+5cos2θ is………
View SolutionLeg f(x)=log((log)1/3((log)13((log)7(sinx+a))) be defined for every real value of x, then the possible value of a is 3 (b) 4 (c) 5 (d) 6
View SolutionThe number of integral values of a for which f(x)=log((log)13((log)7(sinx+a))) is defined for every real value of x is ________
View SolutionThe maximum integral values of x in the domain of f(x)=log10(log1/3(log4(x−5)) is :
View SolutionIf range of f(x)=(lnx)(lnx2)+lnx3+3ln2x+lnx2+2 can be expressed as [ab,cd] where a,b,c and d are prime numbers (not nacessarily distinct) then find the value of (a+b+c+d)2.
View SolutionLet f(x) be a function such that f'(x)=log1/3(log3(sinx+a)). The complete set of values of 'a' for which f(x) is strictly decreasing for all real values of x is:
View SolutionLet f(x)=ln(x−1)(x−3) and g(x)=ln(x−1)+ln(x−3) then,
View SolutionLet f(x)=log(log)13((log)7(sinx+a))) be defined for every real value of x, then the possible value of a is 3 (b) 4 (c) 5 (d) 6
View SolutionLet f(x)=log1/3((log)13((log)7(sinx+a)) be defined for every real value of x, then the possible value(s) of a is (a) 3 (b) 4 (c) 5 (d) 6
View SolutionThe number of integral values of a for which f(x)=log((log)13((log)7(sinx+a))) is defined for every real value of x is ________
View SolutionLet f(x)=log(log1/3(log7(sinx+a))) be defined for every real value of x, then the possible value of a is
View SolutionIf range of f(x)=(lnx)(lnx2)+lnx3+3ln2x+lnx2+2 can be expressed as [ab,cd] where a,b,c and d are prime numbers (not nacessarily distinct) then find the value of (a+b+c+d)2.
View Solution
