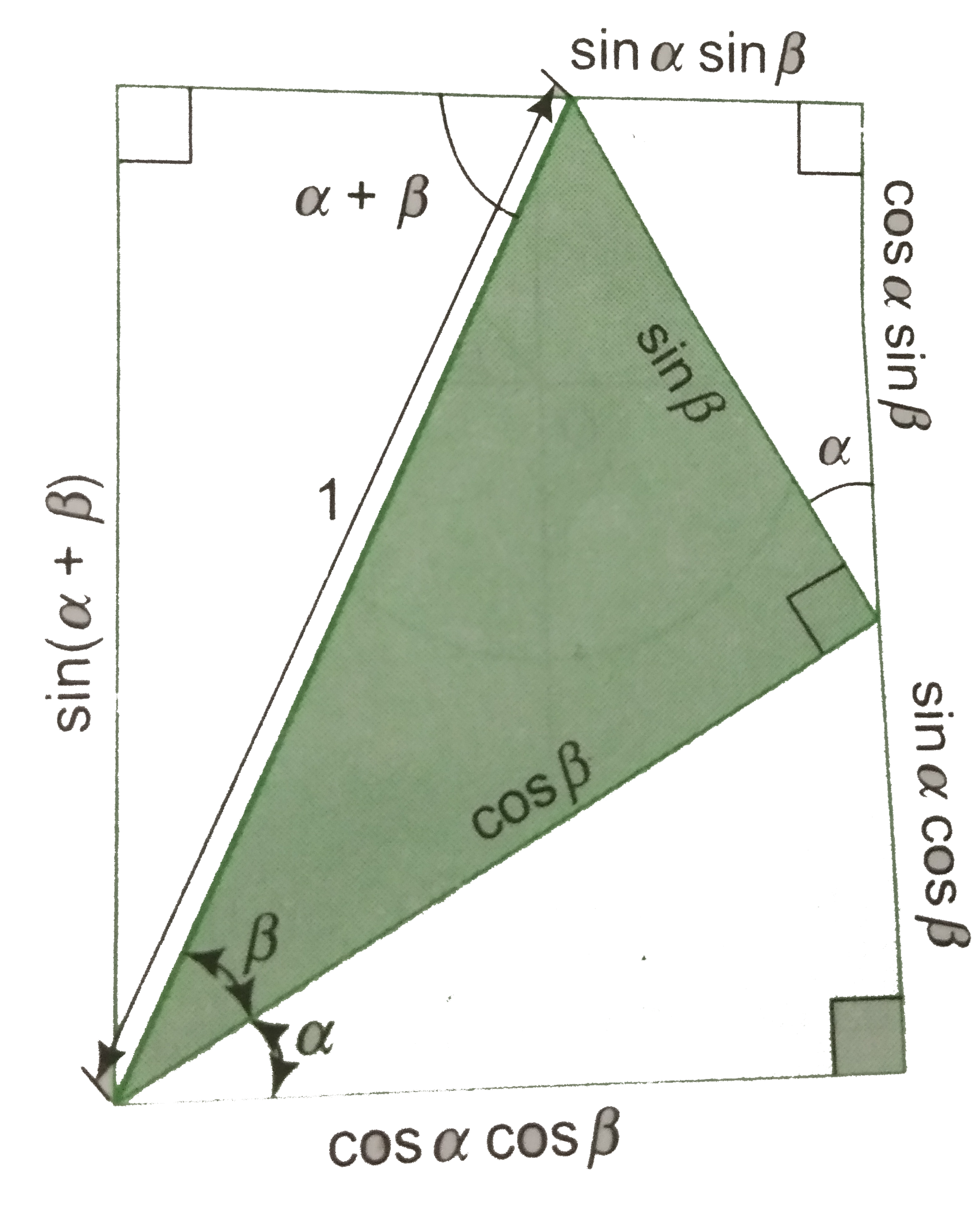
By geometrical interpretation, prove that sin(α+β)s∈αcosβ+sinβcosα cos(α+β)=cosαcosβ−sinαsinβSolution in Bengali
Topper's Solved these Questions
- TRIGONOMETRIC FUNCTIONS BOOK - CENGAGE PUBLICATIONCHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - example
10 Videos
- TRIGONOMETRIC FUNCTIONS BOOK - CENGAGE PUBLICATIONCHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - Concept Application Exercises 2.1
8 Videos
- TRIGONOMETRIC EQUATIONSBOOK - CENGAGE PUBLICATIONCHAPTER - TRIGONOMETRIC EQUATIONSEXERCISE - Archives (Numerical value type)
4 Videos
- TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULASBOOK - CENGAGE PUBLICATIONCHAPTER - TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULASEXERCISE - Archives (Numerical Value Type)
2 Videos
Similar Questions
If 2cosx+sinx=1, then find the valie of 7x+6sinx.
View SolutionTwo sides of a parallelogram are 12 cm and 8 cm. If one of the interior angles is 135∘, then find area of the parallelogram.
View SolutionThe number of all possible values of θ, where 0<θ<π, for which the system of equations (y+z)cos3θ=(xyz)sin3θ,xsin3θ=2cos3θy+2sin3θzand(xyz)sin3θ=(y+2z)cos3θ+ysin3θ have a solution (x0,y0,z0) wiith y0z0≠0 is
View SolutionThe maximum value of the expression 1sin2θ+3sinθcosθ+5cos2θ is………
View SolutionProve by vector methods that sin(alpha+beta)=sin alpha cos beta+cos alpha sin beta
View SolutionBy geometrical interpretation, prove that
(i) sin(α+β)=sinαcosβ+sinβcosα
(ii) cos(α+β)=cosαcosβ−sinαsinβ
View Solutionसिद्ध करे की (sinα.cosβ+cosα.sinβ)2+(cosα.cosβ−sinα.sinβ)2=1
View Solutionसदिश विधि द्वारा सिद्ध कीजिए कि sin(α−β)=sinαcosβ−cosαsinβ
View SolutionIf cosθ=cosαcosβ1+sinαsinβ, show that , sinθ=±sinα+sinβ1+sinαsinβ.
View SolutionUsing vector method, prove cos(α−β)=cosαcosβ+sinαsinβ.
View Solutionयदि A=[cosαsinαsinαcosα] तथा B=[cosβsinβsinβcosβ] तो सिद्ध कीजिए कि AB=BA.
View SolutionProve thatcos(α+β)=cosαcosβ−sinαsinβ
View SolutionBy vector method, prove that cos (α+Bη)=cosαcosBη−sinαsinBη .
View SolutionBy geometrical interpretation, prove that
(i) sin(α+β)=sinαcosβ+sinβcosα
(ii) cos(α+β)=cosαcosβ−sinαsinβ
View SolutionProve that
cos2(α−β)+cos2β−2cos(α−β)cosαcosβ is independent of β.
View SolutionProve that (sinαcosβ+cosαsinβ)2+(cosαcoaβ−sinαsinβ)2=1.
View Solution