Find the height of the regular pyramid with each edge measuring l cm.
Also,
if $α$ is angle between any edge and face not containing that edge, then prove that $cos α = \frac{1}{\sqrt{3}}$
Solution in Bengali

Video Solution

Text Solution

Verified by Experts

In the figure we have regular pyramid.

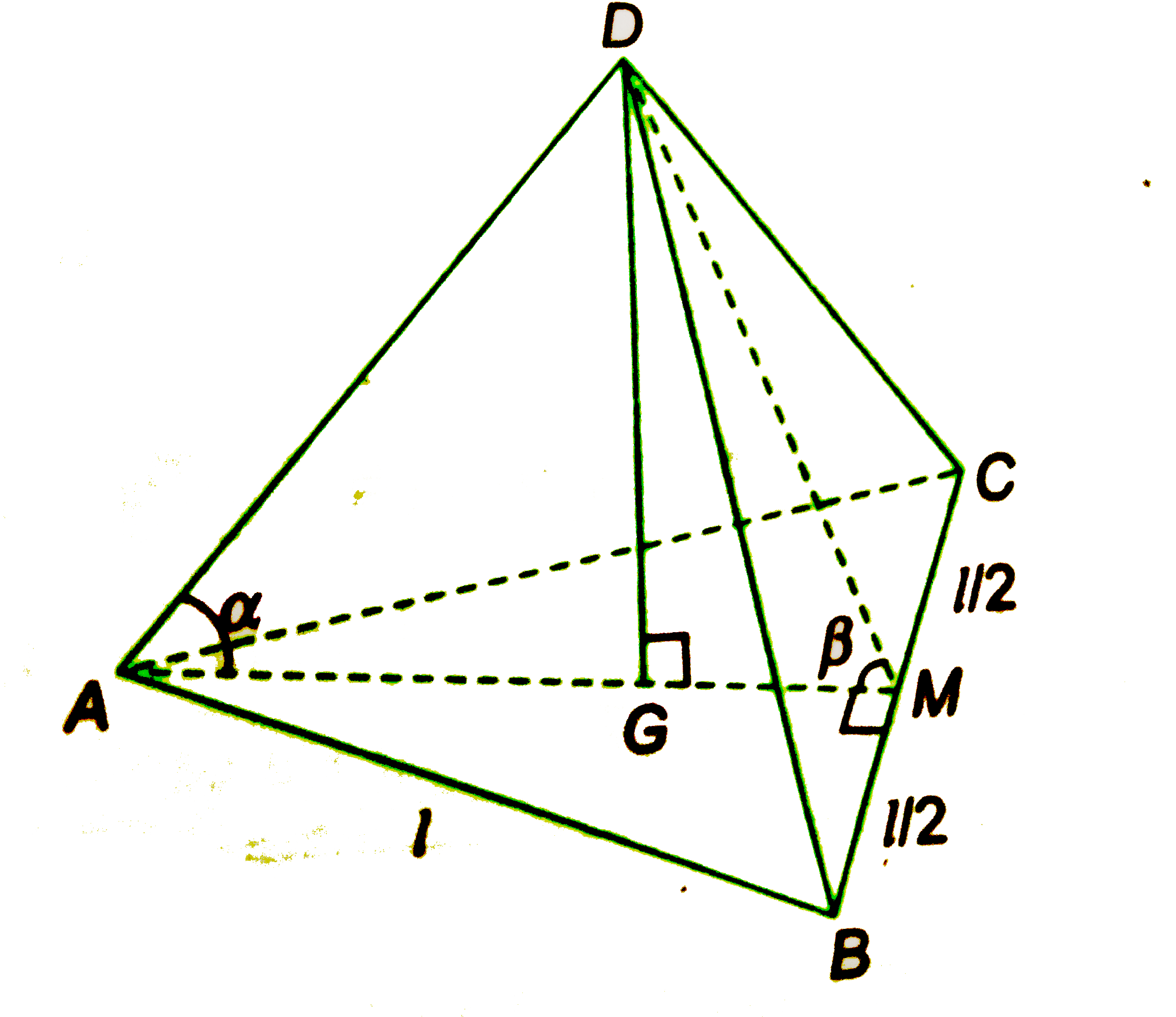
All the edges have length l cm.
So, each face of the pyramid is an equilateral triangle.
From vertex D drop perpendicular to meet opposite face ABC at point G, which is the centre of the triangle ABC.
Here, G is also centroid of triangle ABC as it an equailateral triangle.
Clearly, $A G = \frac{2}{3} A M$
In triangle $A M B, A M = A B {sin 60}^{\circ} = \frac{\sqrt{3}}{2} l c m$
$∴ A G = \frac{2}{3} \times A M = \frac{2}{3} \times \frac{\sqrt{3}}{2} l = \frac{1}{2 \sqrt{3}} lcm$
In triangle AGD, using Pythagoras, we get
$A D^{2} = A G^{2} + G D^{2}$
$∴ l^{2} = \frac{1}{3} l^{2} + G D^{2}$
$∴ G D = \sqrt{\frac{2}{3}} 1 c m$
For angle between any edge and face not containing that edge, consider edge AD and face ABC.
Angle between them is $α$ ,which is angle between AD and AM.
In triangle AGD, $cos α = \frac{A G}{A D} = \frac{\frac{1}{\sqrt{3}} l}{l} = \frac{1}{\sqrt{3}}$
Angle between two faces ABC and BCD is the angle between AM and DM, which is $β$ .
In triangle $D G M, cos β = \frac{G M}{D M} = \frac{1}{3}$

Updated on:21/07/2023

|

Class 12 MATHS TRIGONOMETRIC FUNCTIONS

Topper's Solved these Questions

Similar Questions

CENGAGE PUBLICATION-TRIGONOMETRIC FUNCTIONS -SINGLE CORRECT ANSWER TYPE

Home
Ask Doubt
Profile