The straight line through a fixed point (2,3) intersects the coordinate axes at distinct point P and Q. If O is the origin and the rectangle OPRQ is completed then the locus of R isSolution in Bengali
3x+2y=6xy
3x+2y=6
2x+3y=xy
3x+2y=xy
The correct Answer is:D
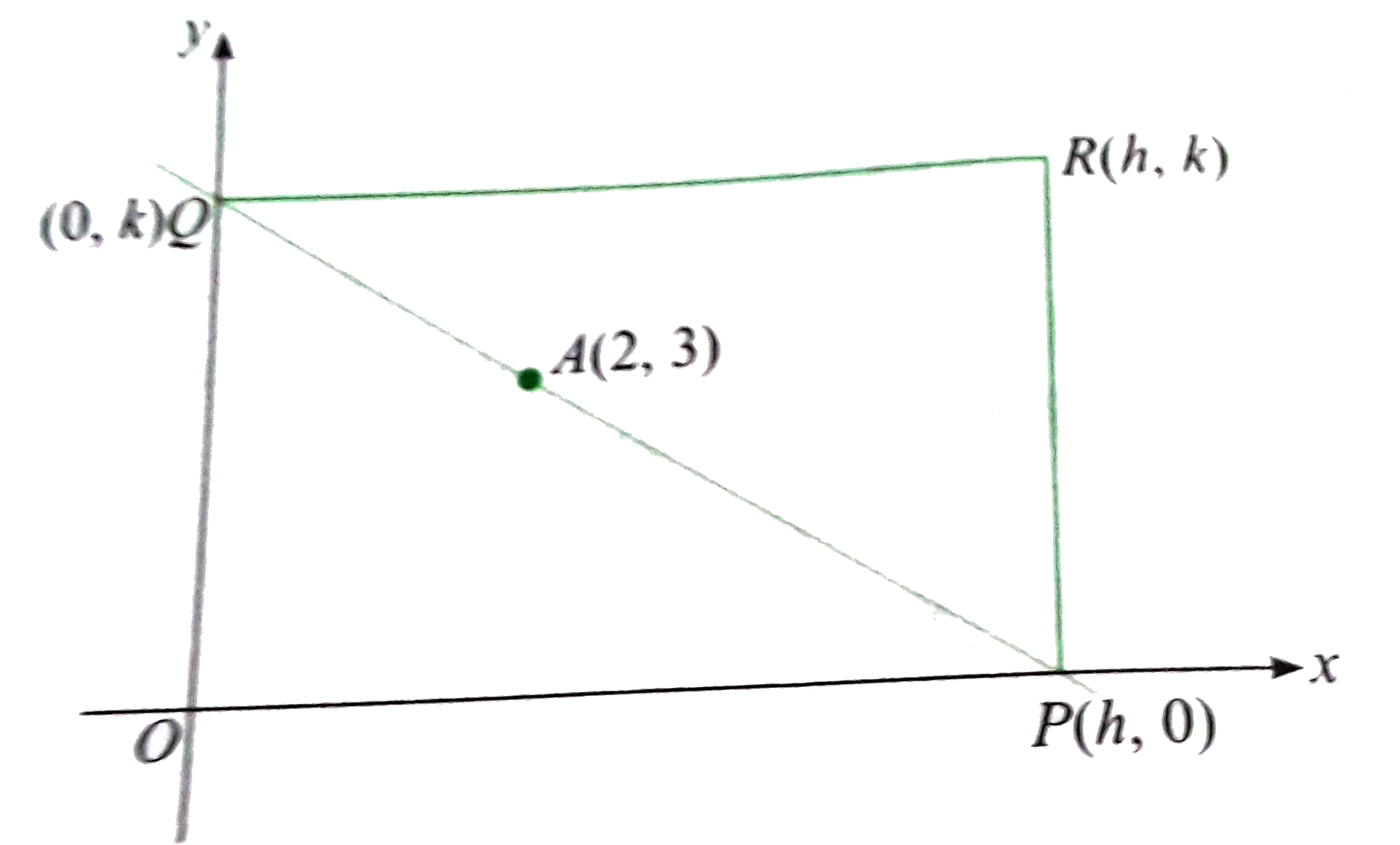
Let the point R be (h,k) .
thus P≡(h,0)andQ≡(0,k)
Equation of variable line PQisxh+yk=1
Point A(2,3) lies on the variable line PQ
∴2h+3k=1
or 2x+3y=1
Therefore, the locus of point R is 2y+3x=xy.
Topper's Solved these Questions
- COORDINATE SYSYEM BOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSYEM EXERCISE - Numerical value
12 Videos
- COORDINATE SYSTEMBOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSTEMEXERCISE - Multiple Correct Answers Type
2 Videos
- CROSS PRODUCTS BOOK - CENGAGE PUBLICATIONCHAPTER - CROSS PRODUCTS EXERCISE - DPP 2.2
13 Videos
Similar Questions
Line AB passes through point (2,3) and intersects the positive x and y-axes at A(a,0) and B(0,b) respectively. If the area of ΔAOB is 11. then the value of 4b2+9a2 is
View SolutionCoordinates of points on curve 5x2−6xy+5y2−4=0 which are nearest to origin are
View SolutionLet →a and →b be two vectors of equal magnitude 5 units. Let →p,→q be vectors such that →p=→a−→b and →q=→a+→b. If |→p×→q|=2{λ−(→a.→b)2}12, then value of λ is
View SolutionThe straight line through a fixed point (2,3) intersects the coordinate axes at distinct point P and Q. If O is the origin and the rectangle OPRQ is completed then the locus of R is
View SolutionA variable line intersects the co-ordinate axes at A and B and passes through a fixed point (a,b). then the locus of the vertex C of the rectangle OACB where O is the origin is
View SolutionA variable plane at constant distance p form the origin meets the coordinate axes at P,Q, and R. Find the locus of the point of intersection of planes drawn through P,Q, r and parallel to the coordinate planes.
View SolutionThe locus of the centre of the circle passing through the origin O and the points of intersection A and B of any line through (a, b) and the coordinate axes is
View Solutionएक सरल रेखा, जो एक अचर बिन्दु (2,3) से होकर जाती है, निर्देशांक अक्षों को दो विभिन्न बिन्दुओं P तथा Q पर प्रतिच्छेद करती है। यदि ० मूल बिन्दु है तथा आयत OPRQ को पूरा किया जाता है, तो R का बिन्दूपथ है
View SolutionA variable line passing through a fixed point (α,β) intersects the coordinate axes at A and B. If O is the origin, then the locus of the centroid of the ΔOAB is
View SolutionA variable line intersects the co-ordinate axes at A and B and passes through a fixed point (a, b), then the locus of the vertex C of the rectangle OACB where O is the origin is :
View Solution(2,3) বিন্দুগামী একটি সরলরেখা স্থানাঙ্ক অক্ষদ্বয়কে দুটি ভিন্ন বিন্দু P ও Q-তে ছেদ করে। যদি O মূলবিন্দু হয় এবং OPRQ একটি আয়তক্ষেত্র গঠিত হয়, তবে R বিন্দুর সঞ্চারপথ হয়—
View SolutionA straight line, which passes through a constant point (2,3), intersects the coordinate axes at two different points P and Q. If 0 is the root point and the rectangle OPRQ is met, then the point of R is
View SolutionThe straight line through a fixed point (2,3) intersects the coordinate axes at distinct point P and Q. If O is the origin and the rectangle OPRQ is completed then the locus of R is
View SolutionLine passess from fixed point (2,3) intersects axis of points P and Q. If O is origin and OPRQ will be rectangle then locus of point R is ..........
View SolutionThe straight line through a fixed point (2,3) intersects the coordinate axes at distinct point P and Q. If O is the origin and the rectangle OPRQ is completed then the locus of R is
View SolutionThe locus of the centre of the circle passing through the origin O and the points of intersection A and B of any line through (a, b) and the coordinate axes is
View Solution
