If O is the origin and if the coordinates of any two points Q1 and Q2 are (x1,y1) and (x2,y2), respectively, prove that OQ1.OQ2cos∠Q1OQ2=x1x2+y1y2.Solution in Bengali
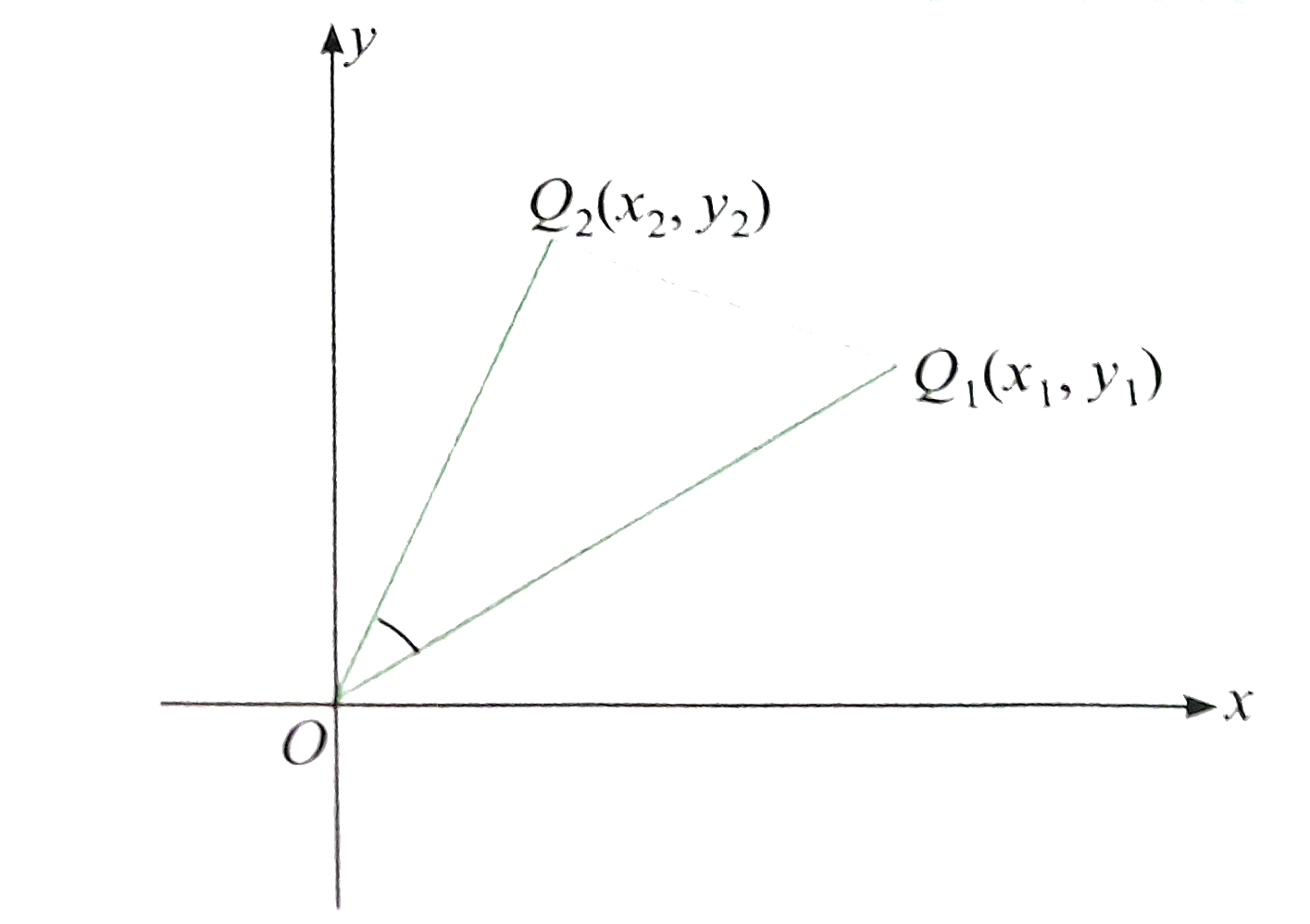
In ΔOQ1Q2, using cosing rule, we get
(Q−1Q2)2=(OQ1)2+(OQ2)2−OQ1.OQ2.cos(∠Q1OQ2)
∴(x2−x1)2+(y2−y1)2
=(x21+y21)+(x22+y22)−2OQ1.OQ2.cos(∠Q1OQ2)
⇒OQ1.OQ2cos(∠Q1OQ2)=x1x2+y1y2.
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSYEM EXERCISE - Illustration1.141videos
COORDINATE SYSYEM
- BOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSYEM EXERCISE - Illustration1.151videos
COORDINATE SYSYEM
- BOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSYEM EXERCISE - Illustration1.121videos
COORDINATE SYSYEM
- BOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSTEMEXERCISE - Multiple Correct Answers Type2videos
COORDINATE SYSTEM
- BOOK - CENGAGE PUBLICATIONCHAPTER - CROSS PRODUCTS EXERCISE - DPP 2.213videos
CROSS PRODUCTS
Similar Questions
Given that P(3,1),Q(6.5), and R(x,y) are three points such that the angle PQR is a right angle and the area of RQP is 7,
find the value of 4x−3y+503:06View SolutionFind the area of a triangle whose vertices are A(3,2),B(11,8)andC(8,12).
03:05View SolutionTwo points O(0,0) and A(3,√3) with another point P form an equilateral triangle. Find the coordinates of P.
02:27View SolutionCoordinates of points on curve 5x2−6xy+5y2−4=0 which are nearest to origin are
05:02View SolutionLet →a and →b be two vectors of equal magnitude 5 units. Let →p,→q be vectors such that →p=→a−→b and →q=→a+→b. If |→p×→q|=2{λ−(→a.→b)2}12, then value of λ is
02:36View SolutionThe coordinates of two points PandQ are (x1,y1)and(x2,y2)andO is the origin. If the circles are described on OPandOQ as diameters, then the length of their common chord is |x1y2+x2y1|PQ (b) |x1y2−x2y1|PQ |x1x2+y1y2|PQ (d) |x1x2−y1y2|PQ
03:04View SolutionLet A and B have coordinates (x_1,y_1) and (x_2,y_2) respectively. We define the distance between A and B as d(A,B) =max||x_2-x_1|,|y_2-y_1|| If d(A,O)=1 where O is the origin then locus of A has an area of
View SolutionIf the line segment joining the points P(x1,y1)and Q(x2,y2) subtends an angle α at the origin O, prove that : OP.OQ cosα=x1x2+y1y2.
03:33View SolutionIf θ is the angle which the straight line joining the points (x1,y1)and (x2,y2) subtends at the origin, prove that tanθ=x2y1−x1y2x1x2+y1y2 andcosθ=x1x2+y1y2√x12+y12x22+y22
04:04View SolutionThe electric force on a charge q1 due to q2 is (4ˆi−3ˆj)N. What is the force on q2 due to q1?
04:24View SolutionIn previous question the ratio of heat flow at M and N are Q_1 and Q_2 respectively. Then –
02:08View SolutionIf the coordinates of any two points Q1andQ2 are (x1,y1) and (x2,y2), respectively, then prove that OQ1×OQ2cos(∠Q1OQ2)=x1x−2+y−1y2, whose O is the origin.
04:00View Solution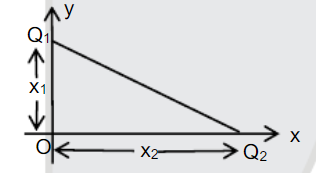
Two charge Q1 and Q2 are placed in xy plane at a distance x1 and x2 from origin a shown in figure. if electric field at O is same for both charge then find ratio Q1 and Q2.07:23View SolutionIf O is the origin and if the coordinates of any two points Q1 and Q2 are (x1,y1) and (x2,y2), respectively, prove that OQ1.OQ2cos∠Q1OQ2=x1x2+y1y2.
01:35View SolutionThe coordinates of two points PandQ are (x1,y1)and(x2,y2)andO is the origin. If the circles are described on OPandOQ as diameters, then the length of their common chord is (a)|x1y2+x2y1|PQ (b) |x1y2−x2y1|PQ |x1x2+y1y2|PQ (d) |x1x2−y1y2|PQ
01:59View SolutionIf the coordinates of any two points Q1andQ2 are (x1,y1) and (x2,y2), respectively, then prove that OQ1×OQ2cos(∠Q1OQ2)=x1x−2+y−1y2, whose O is the origin.
07:06View Solution