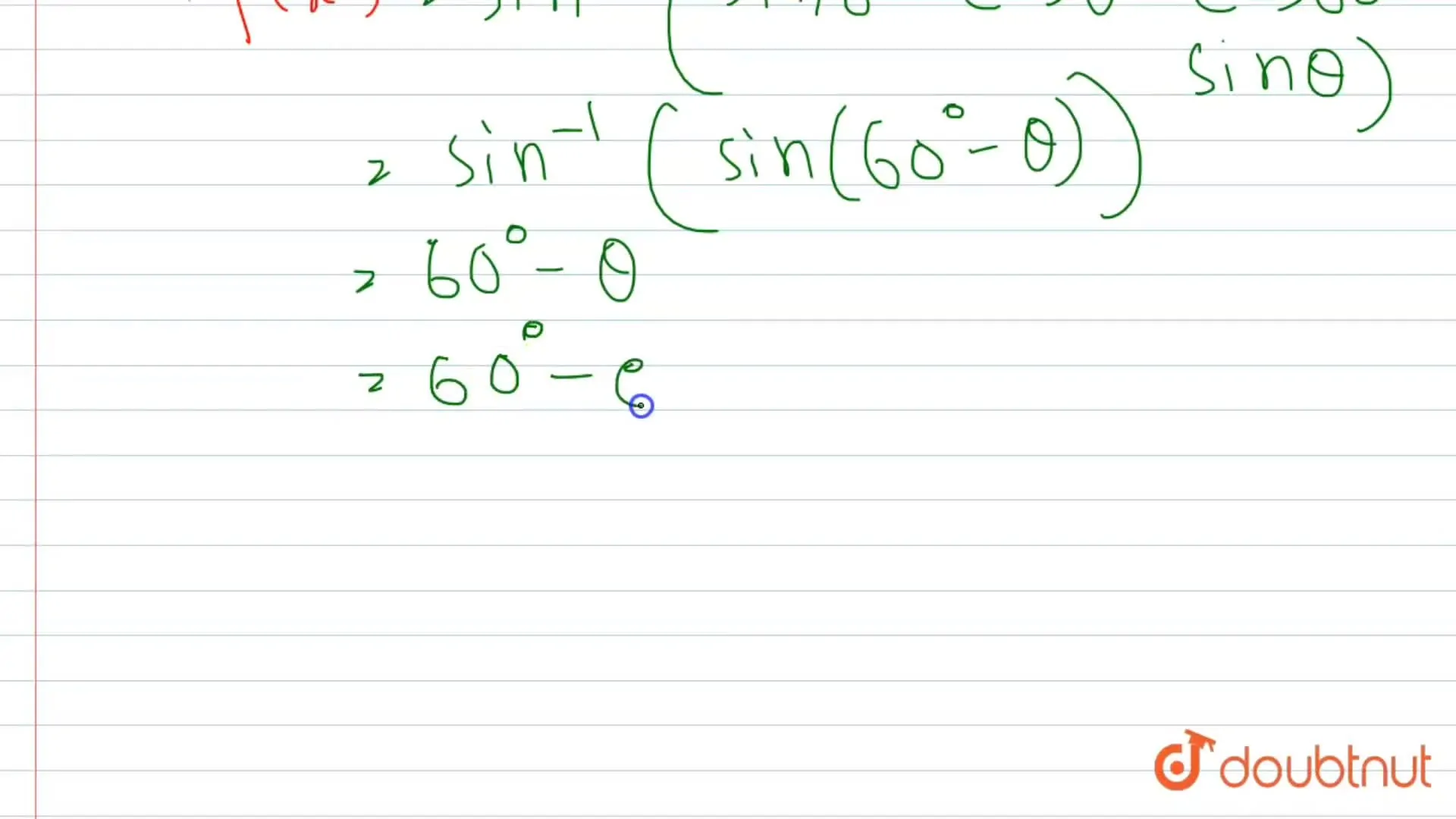If f(x)=sin−1(√32x−12√1−x2),−12≤x≤1,thenf(x) is equal to sin−1(12)−sin−1(x) sin−1x−π6 sin−1x+π6 (d) none of theseSolution in Bengali
sin−1(12)−sin−1(x)
sin−1x−π6
sin−1x+π6
none of these
The correct Answer is:B
Let x=sinθ, where −12≤x≤1
or −π6≤θ≤π2. Then,
f(x)=sin−1(√32x−12√1−x2)
=sin−1(√32sinθ−12cosθ)
=sin−1(sin(θ−π6))
=θ−π6=sin−1x−π6 [∵θ−π6∈(−π3,π3)]
Related Playlists
Similar Questions
The points with position vectors →x+→y,→x−→yand→x+λ→y are collinear for all real values of λ.
03:26View SolutionIf y = y(x) is the solution of the differential equation, xdydx+2y=x2 satisfying y(1) = 1, then y(12) is equal to
01:49View SolutionIf f(x)=2sin−1√1−x+sin−1(2√x(1−x)) , where x∈(0,12),thenf′(x) is (a)2√x(1−x) (b) zero (c)−2√x(1−x) (d) π
02:31View SolutionIf sin−1x−cos−1x=π6 , then x= 12 (b) √32 (c) −12 (d) none of these
01:12View Solutionsin^(-1)sqrt(x^(2)+2x+1)+sec^(-1)sqrt(x^(2)+2x+1)=(pi)/(2);x!=0 then the value of 2sec^(-1)((x)/(2))+sin^(-1)((x)/(2)) is equal to
04:13View SolutionA solution of sin−1(1)−sin−1(√3x2)−π6=0 is (A) x=−√2 (B) x=√2 (C) x=2 (D) x=1√2
04:21View SolutionIf f (x) = tan ^(-1)sqrt((1 + sin x )/(1 - sin x)), 0 le x le (pi)/(2) then f' ((pi)/(6)) =?
03:04View SolutionSolve for x :
i) cos(sin−1x)=12
ii) tan−1x=sin−11√2
iii) sin−1x−cos−1x=π605:54View Solutionsin−1√3x+sin−1x=π2
03:22View SolutionIf x∈(π,3π2) then the value of tan−1(√1−sinx+√1+sinx√1−sinx−√1+sinx)
03:38View SolutionIf f(x)=sin−1(√32x−12√1−x2),−12≤x≤1,thenf(x) is equal to
03:05View SolutionIf f(x)=sin−1(√32x−12√1−x2),−12≤x≤1,thenf(x) is equal to sin−1(12)−sin−1(x) sin−1x−π6 sin−1x+π6 (d) none of these
09:20View SolutionIf sin−1x−cos−1x=π6 , then x= (a)12 (b) √32 (c) −12 (d) none of these
08:20View SolutionDifferentiate w.r.t x : cot−1{√1+sinx+√1−sinx√1+sinx−√1−sinx},0<x<π2
02:54View SolutionDifferentiate w.r.t x : tan−1{√1+sinx+√1−sinx√1+sinx−√1−sinx},0<x<π2
03:02View SolutionIf f(x) = sin−1x√1−x2, g(x)=esin−1x, then ∫ f(x)g(x) dx =........................ A) esin−1x(sin−1x−1)+c B) esin−1x(1−sin−1x)+c C) esin−1x(sin−1x+1)+c D) −esin−1x(sin−1x−1)+c
01:49View Solution