If 2x−y+1=0 is a tangent to the hyperbola x2a2−y216=1 then which of the following CANNOT be sides of a right angled triangle?Solution in Bengali
(a) 2a, 4, 1
(b) 2a, 8, 1
(c) a, 4, 1
(d) a, 4, 2
The correct Answer is:B, C, D
The line y=mx+c is tangent to hyperbola x2a2−y2b2=1.
if c2=a2m2−b2.
Given tangent is : y=2x+1
∴ (1)2=4a2−16
⇒ a2=174
⇒ a2=√172
For option (1), sides are √17,4,1, which form right angled triangle.
For option (2), sides are √17,8,1,, for which triangle is not possible.
For option (3), sides are √172,4,1, for which triangle is not possible.
For option (4), sides are √172,4,2, for which triangle exists but not right angled.
Topper's Solved these Questions
- HYPERBOLABOOK - CENGAGE PUBLICATIONCHAPTER - HYPERBOLAEXERCISE - COMPREHENSION TYPE
2 Videos
- HYPERBOLABOOK - CENGAGE PUBLICATIONCHAPTER - HYPERBOLAEXERCISE - JEE MAIN
3 Videos
- HIGHT AND DISTANCE BOOK - CENGAGE PUBLICATIONCHAPTER - HIGHT AND DISTANCE EXERCISE - Archives
3 Videos
- INDEFINITE INTEGRATIONBOOK - CENGAGE PUBLICATIONCHAPTER - INDEFINITE INTEGRATIONEXERCISE - Multiple Correct Answer Type
2 Videos
Similar Questions
The circle x2+y2−8x=0 and hyperbola x29−y24=1 I intersect at the points A and B. Equation of a common tangent with positive slope to the circle as well as to the hyperbola is (A) 2x−√5y−20=0 (B) 2x−√5y+4=0 (C) 3x−4y+8=0 (D) 4x−3y+4=0
View SolutionThe eccentricity of the hyperbola whose latus rectum is 8 and conjugate axis is equal to half the distance between the foci is
View SolutionA bird is sitting on the top of a vertical pole 20 m high and its elevation from a point O on the ground is 45o . It flies off horizontally straight away from the point O. After one second, the elevation of the bird from O is reduced to 30o . Then the speed (in m/s) of the bird is (1) 40(√2−1) (2) 40(√3−2) (3) 20√2 (4) 20(√3−1)
View SolutionIf ∫e4x−1e2xlog(e2x+1e2x−1)dx=t22logt−t24−u22logu+u24+C, then
View SolutionIf 2x−y+1=0 is a tangent to the hyperbola x2a2−y216=1 then which of the following CANNOT be sides of a right angled triangle? (a)a,4,2 (b) a,4,1 (c)2a,4,1 (d) 2a,8,1
View SolutionIf 2x−y+1=0 is a tangent to hyperbola x2a2+y216=1, then which of the following are sides of a right angled triangle ?
View SolutionThe slopes of the common tangents of the hyperbolas x29−y216=1 and y29−x216=1, are
View SolutionThe area of triangle formed by the lines x−y=0,x+y=0 and any tangent to the hyperbola x2−y2=16 is equal to
View Solutionयदि 2x−y+1=0 अतिपरवलय x2a2−y216=1 की स्पर्शरेखा है तो निम्न में से कौनसी समकोणीय त्रिभुज की भुजायें नहीं हो सकती है (हैं)
View SolutionIf 3x+2y−1=0 is a tangent to a hyperbola x216−y29=1, then the point of contact is
View SolutionHyperbola x^2/(25)-y^2/(16)=1 The line that follows 2x+y=1 Is perpendicular to, the equation of is
View SolutionIf 2x−y+1=0 is a tangent to the hyperbola x2a2−y216=1 then which of the following CANNOT be sides of a right angled triangle?
View Solutionआकृति में यदि ABIICD,∠APQ=50∘और∠PRD=127∘ है, तो Y का मान है-
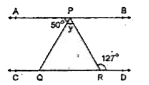
View Solutionयदि 2x−y+1=0 अतिपरवलय x2a2−y216=1 की स्पर्शरेखा है तो निम्न में से कौनसी समकोणीय त्रिभुज की भुजायें नहीं हो सकती है (हैं)
View SolutionTangents drawn from a point on the circle x2+y2=9 to the hyperbola x225−y216=1,
then tangents are at angle
View Solution
