The lines L1:y-x =0 and L2: 2x+y =0 intersect the line L3 : y+2 =0 at P and Q respectively. The bisector of the acute angle between L1 and L2 intersects L3 at R
Statement - 1 : The ratio PR : PQ equals 2√2:√5
Statement - 2 : In any triangle , bisector of an angle divides the triangle into two similar triangle Solution in Bengali
Statement 1 is true, statement 2 is false.
Statement 1 is true, statement 2 is true, statement 2 is the correct explanation of statement1.
Statement 1 is true, statement 2 is true, statement 2 is not the correct explanation of statement 1.
Statement 1 is false, statement 2 is true.
The correct Answer is:A
Draw lines on coordinate axes as shown here.
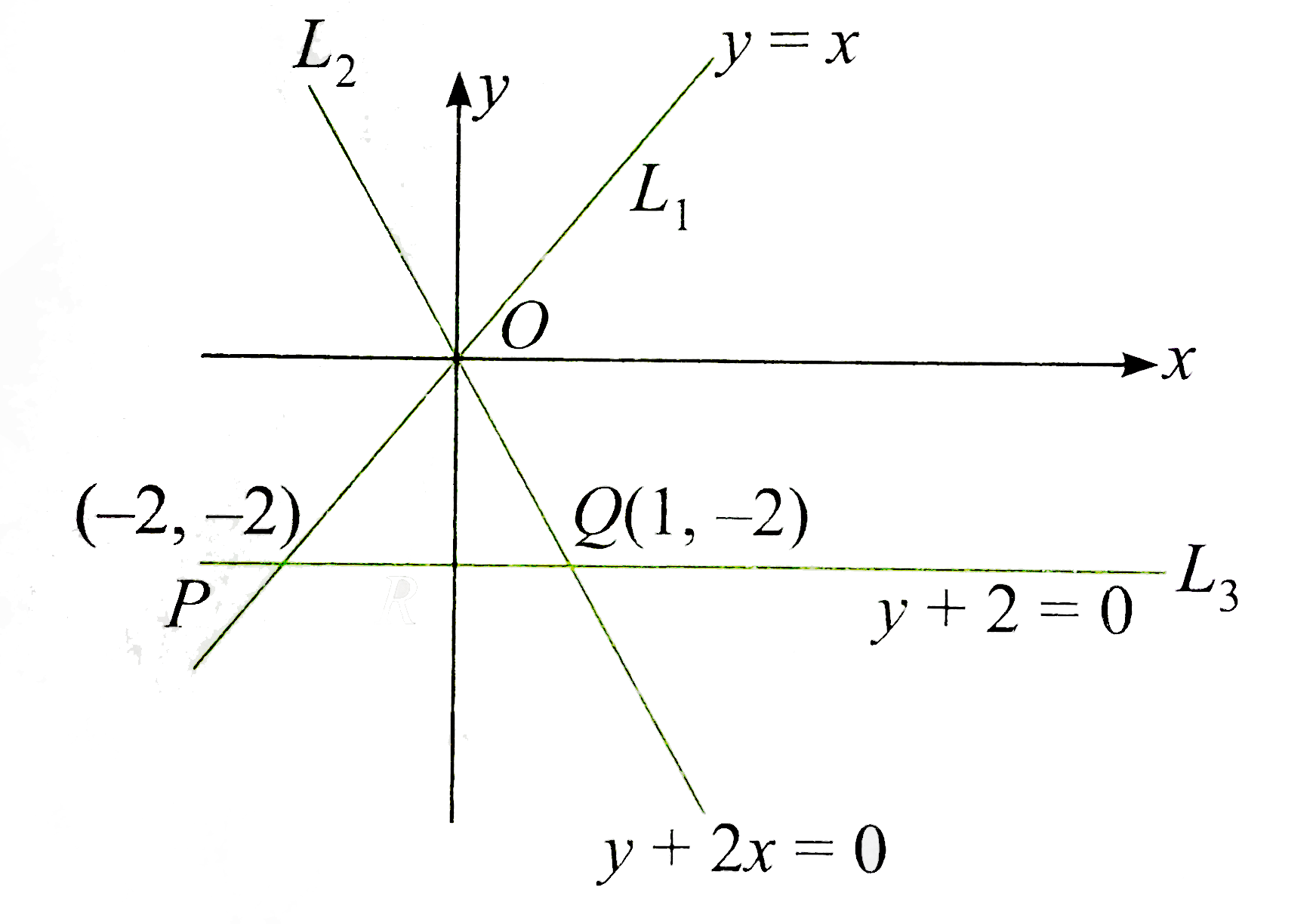
From the geometry of angle bisector,
PRRQ=OPOQ=2√2√5
Topper's Solved these Questions
- STRAIGHT LINESBOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - ARCHIVES (JEE ADVANCED)
3 Videos
- STRAIGHT LINESBOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - ARCHIVES (NUMERICAL VALUE TYPE)
1 Videos
- STRAIGHT LINESBOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - EXERCISE (NUMERICAL VALUE TYPE)
13 Videos
- STRAIGHT LINEBOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type
8 Videos
- THEORY OF EQUATIONSBOOK - CENGAGE PUBLICATIONCHAPTER - THEORY OF EQUATIONSEXERCISE - JEE ADVANCED (Numerical Value Type )
1 Videos
Similar Questions
The locus of the orthocentre of the triangle formed by the lines (1+p)x−py+p(1+p)=0,(1+q)x−qy+q(1+q)=0 and y = 0, where p≠⋅q, is (A) a hyperbola (B) a parabola (C) an ellipse (D) a straight line
View SolutionFor a point P in the plane, let d1(P)andd2(P) be the distances of the point P from the lines x−y=0andx+y=0 respectively. The area of the region R consisting of all points P lying in the first quadrant of the plane and satisfying 2≤d1(P)+d2(P)≤4, is
View SolutionFind the number of permutations of the set {1,2,3,4} in which no two adjacent positions are filled by consecutive integers ( increasing orders).
View SolutionThe point P(α,α+1) will lie inside the triangle whose vertices are A(0,3),B(−2,0) and C(6,1) if
View SolutionThe number of distinct real roots of x4−4x3+12x2+x−1=0is_____.
View SolutionThe lines L_(1): y-x=0 " and " L_(2): 2x+y=0 intersect the line L_(3):y+2=0 at P and Q, respectively. The bisector of the acute angle between L_(1) " and " L_(2) " intersects " L_(3) at R. Statement 1 : The ratio PR : RQ equals 2sqrt(2) : sqrt(5). Statement 2: In any triangle, bisector of an angle divides the triangle into two similar triangles.1
View SolutionLines L_(1) : y-c=0 and L_(2) : 2x+y=0 intersect the line L_(3) : y+2=0 at P and Q respectively. The bisector of the acute angle between L_(1) and L_(2) intersects L_(3) at R . Statement I The ratio PR : RQ equals 2sqrt(2) : sqrt(5) . Because Statement II In any triangle, bisector of an angle divides the triangle into two similar triangles.
View SolutionThe lines L_(1) : y - x = 0 and L_(2) : 2x + y = 0 intersect the line L_(3) : y + 2 = 0 at P and Q respectively . The bisectors of the acute angle between L_(1) and L_(2) intersect L_(3) at R . Statement 1 : The ratio PR : RQ equals 2sqrt2 : sqrt5 Statement - 2 : In any triangle , bisector of an angle divides the triangle into two similar triangles .
View SolutionConsider the lines given by L1:x+3y−5=0 L2:3x−ky−1=0 L3:5x+2y−12=0 Column I|Column II L1,L2,L3 are concurrent if|p. k=−9 One of L1,L2,L3 is parallel to at least one of the other two if|q. k=−65 L1,L2,L3 form a triangle if|r. k=56 L1,L2,L3 do not form a triangle if|s. k=5
View SolutionThe line L1:y−x=0 and L2:2x+y=0 intersect the line L3:y+2=0 at P and Q respectively. The bisector of the acute angle between L1 and L2 intersects L3 at R. Statement-1 : The ratio PR:RQ equals 2√2:√5 Statement-2 : In any triangle, bisector of an angle divides the triangle into two similar triangles. Statement-1 is true, Statement-2 is true ; Statement-2 is correct explanation for Statement-1 Statement-1 is true, Statement-2 is true ; Statement-2 is not a correct explanation for Statement-1 Statement-1 is true, Statement-2 is false Statement-1 is false, Statement-2 is true
View SolutionThe equations of bisectors of two lines L1&L2 are 2x−16y−5=0 and 64x+8y+35=0. lf the line L1 passes through (−11,4), the equation of acute angle bisector of L1 & L2 is:
View SolutionThe lines L_(1) : y - x = 0 and L_(2) : 2x + y = 0 intersect the line L_(3) : y + 2 = 0 at P and Q respectively . The bisectors of the acute angle between L_(1) and L_(2) intersect L_(3) at R . Statement 1 : The ratio PR : RQ equals 2sqrt2 : sqrt5 Statement - 2 : In any triangle , bisector of an angle divides the triangle into two similar triangles .
View Solutionरेखा L1: y-x = 0 औरL2 : 2x + y = 0, क्रमशः P और Q पर रेखा L3.::y+ 2 = 0 को प्रतिच्छेद करती है।L1 और L2 के बीच के न्यूनकोण का अर्धक, R पर L3 को प्रतिच्छेद करता है।
कथन - 1 : अनुपात PR:RQ=2√2:√5, क्योंकि
कथन -2 : किसी त्रिभुज में, कोण का अर्धक त्रिभुज को दो समान त्रिभुजों में विभाजित करता है।
View SolutionLines L_(1):y-x=0 and L_(2):2x+y=0 intersect the line L_(3) : y+2=0 at P and Q respectively. The bisector of the acute angle between L_(1) and L_(2) intersects L_(3) at R. Statement-I: The ratio PR: RQ equals 2sqrt(2):sqrt(5) because. Statement II: In any triangle bisector of an angle divides the triangle into two similar triangles.
View SolutionThe lines L_1 :y-x =0 and L_2 : 2x+y =0 intersect the line L_3 : y+2 =0 at P and Q respectively. The bisector of the acute angle between L_1 and L_2 intersects L_3 at R Statement - 1 : The ratio PR : PQ equals 2sqrt2 : sqrt5 Statement - 2 : In any triangle , bisector of an angle divides the triangle into two similar triangle
View SolutionThe line L_1:""y""-""x""=""0 and L_2:""2x""+""y""=""0 intersect the line L_3:""y""+""2""=""0 at P and Q respectively. The bisector of the acute angle between L_1 and L_2 intersects L_3 at R. Statement-1 : The ratio P R"":""R Q equals 2sqrt(2):""sqrt(5) Statement-2 : In any triangle, bisector of an angle divides the triangle into two similar triangles. Statement-1 is true, Statement-2 is true ; Statement-2 is correct explanation for Statement-1 Statement-1 is true, Statement-2 is true ; Statement-2 is not a correct explanation for Statement-1 Statement-1 is true, Statement-2 is false Statement-1 is false, Statement-2 is true
View Solution
