Find the values of b for which the points $(2 b + 3, b^{2})$ lies above of the line 3x-4y-a(a-2) = 0 $\forall a \in R$ .Solution in Bengali

Video Solution

Text Solution

Verified by Experts

Given line is 3x-4y-a(a-2)=0
One of the possible lines is as shown in the following figure.

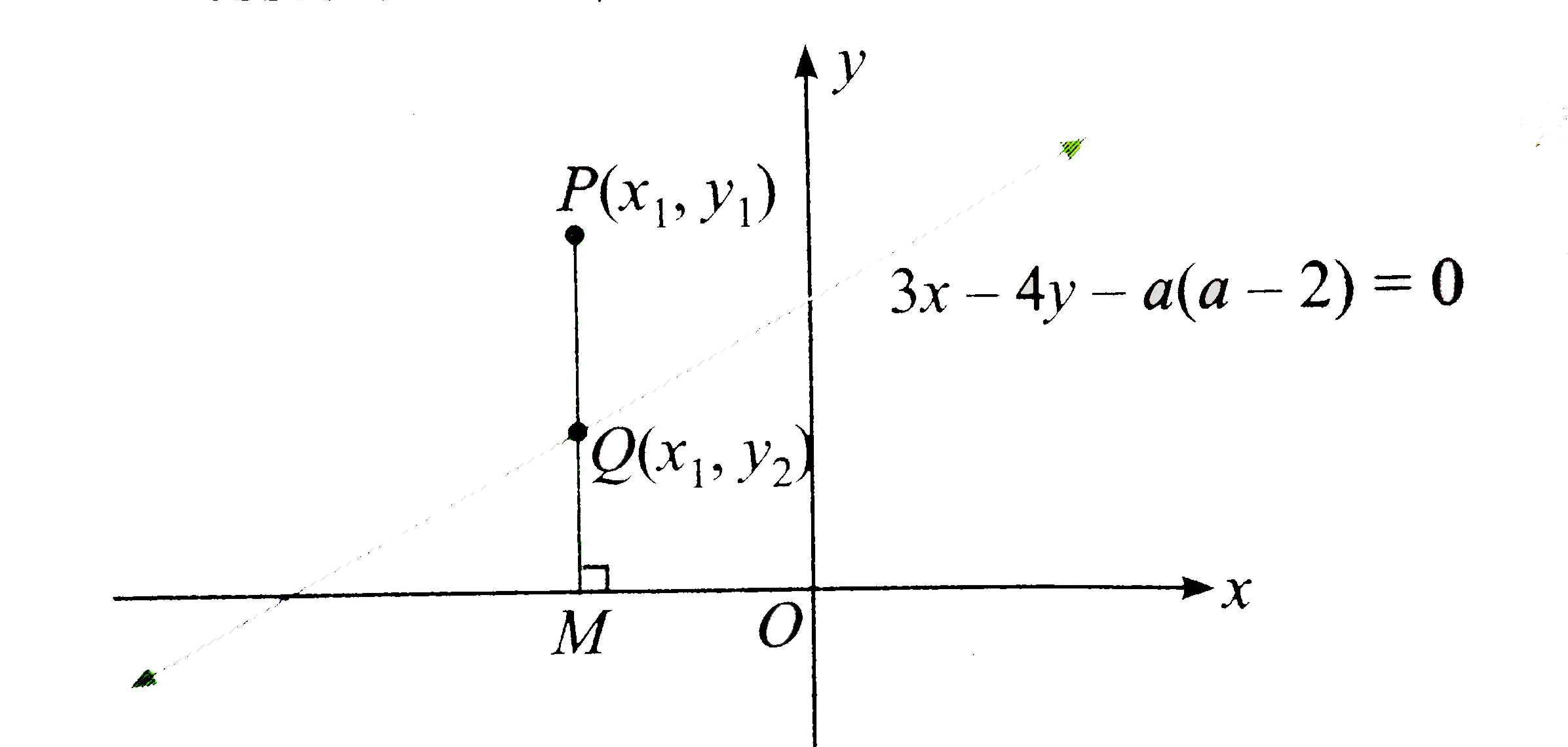
Consider the point $P (x_{1}, y_{1})$ lying above this line.
Draw perpendicular from point P to the x-axis meeting the line at $Q (x_{1}, y_{2}) and x-axis at M$
$Clearly, PM > Q M$
$∴ y_{1} > y_{2}$
$\Rightarrow - 4 y_{1} < - 4 y_{2}$
$\Rightarrow 3 x_{1} - a (a - 2) - 4 y_{1} < 3 x_{1} - a (a - 2) - 4 y_{2}$
$\Rightarrow 3 x_{1} - a (a - 2) - 4 y_{1} < 0 (As point Q lies on the line)$
$\Rightarrow 3 (2 b + 3) - a (a - 2) - 4 b^{2} < 0, \forall a \in R$
$(Putting x_{1} = 2 b + 3 and y_{1} = b^{2})$
$a^{2} - 2 a + 4 b^{2} - 6 b - 9 > 0 \forall a \in R$
$∴ Discriminant < 0$
$\Rightarrow 4 - 4 (4 b^{2} - 6 b - 9) < 0$
$\Rightarrow 1 - 4 b^{2} + 6 b + 9) < 0$
$\Rightarrow 2 b^{2} - 3 b - 5 > 0$
$\Rightarrow (2 b - 5) (b + 1) > 0$
$\Rightarrow b \in (- \infty, - 1) \cup (\frac{5}{2}, \infty)$

Updated on:21/07/2023

|

Class 12 MATHS STRAIGHT LINES

Topper's Solved these Questions

Similar Questions

CENGAGE PUBLICATION-STRAIGHT LINES-ARCHIVES (NUMERICAL VALUE TYPE)

Home
Ask Doubt
Profile