Question

$ABC$
is an equilateral triangle with $A(0,0)$
and $B(a,0)$
, (a>0). L, M and $N$
are the foot of the perpendiculars drawn from a point $P$
to the side $AB,BC,andCA$
, respectively. If $P$
lies inside the triangle and satisfies the condition $P{L}^2=PM\stackrel{.}{P}N,$
then find the locus of $P\stackrel{.}{}$

Explanation

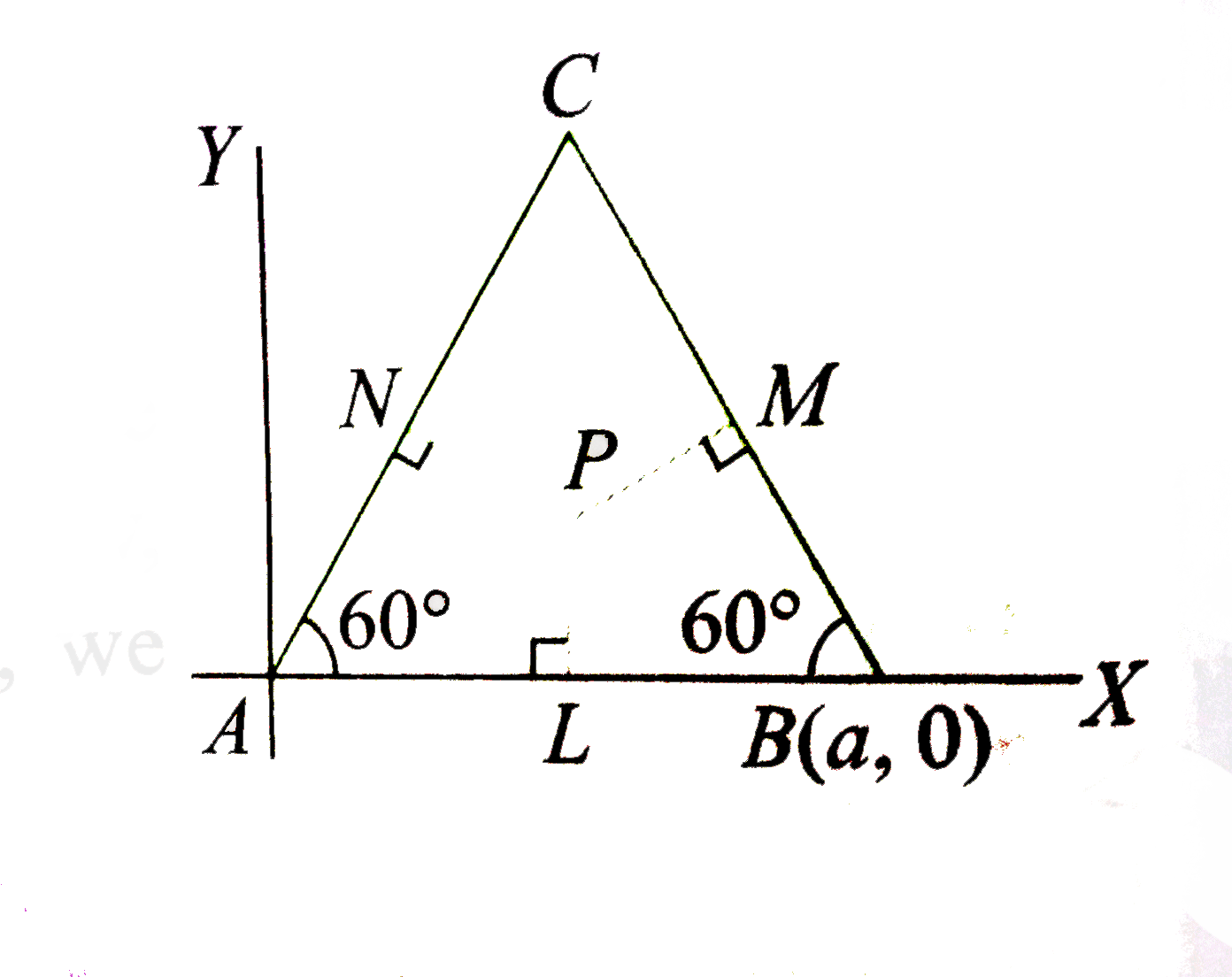
The equations of lines AC and BC are, respectively, given by
`y-sqrt(3) x =0`
`y+sqrt(3)(x-a) =0`
Let P(h,k) be the coordinates of the point whose locus is to be found. Now, according to the given condition, we have
`PL^(2) = PM*PN`
`i.e., k^(2) = (|k-sqrt(3)h|)/(2) * (|k+sqrt(3)(h-a)|)/(2)`
`i.e., 4k^(2) = (k-sqrt(3)h)[k+sqrt(3)(h-a)] " " [because "P lies below both the lines"]`
`i.e., 3(h^(2)+k^(2))-3ah + sqrt(3) ak = 0`
`i.e., h^(2)+k^(2)-ah + (a)/(sqrt(3)) k = 0`
Putting (x,y) in place of (h,k) gives the equation of the required locus as
` x^(2)+y^(2)-ax + (a)/(sqrt(3))y = 0`