Factorise the expression: am2+bm2+bn2+an2 Solution in Bengali
The correct Answer is:a→q;b→r;c→q;d→p.
We know that limx→0sinxx=1 (but a value is smaller than 1)
or [limx→0100sinxx]=99
and [limx→0100xsinx]=100
Also, limx→0sin−1xx=1 (but a value is more than 1)
or [limx→0100sin−1xx]=100
and [limx→0100xsin−1x]=99
limx→0tanxx=1 (but a value is bigger than 1)
or [limx→0100tanxx]=100
and [limx→0100tan−1xx]=99
Hence,
a. limx→0([100sinxx]+[100tanxx])=199
b. limx→0([100xsinx]+[100tanxx])=200
c. limx→0([100sin−1xx]+[100tan−1xx])=199
d. limx→0([100xsin−1x]+[100tan−1xx])=198
Topper's Solved these Questions
- LIMITSBOOK - CENGAGE PUBLICATIONCHAPTER - LIMITSEXERCISE - Numerical Value Type
26 Videos
- LIMITSBOOK - CENGAGE PUBLICATIONCHAPTER - LIMITSEXERCISE - Archives JEE MAIN
8 Videos
- LIMITSBOOK - CENGAGE PUBLICATIONCHAPTER - LIMITSEXERCISE - Linked Comprehension Type
20 Videos
- JEE 2019BOOK - CENGAGE PUBLICATIONCHAPTER - JEE 2019EXERCISE - Chapter 10
8 Videos
- LINEAR COMBINATION OF VECTORS, DEPENDENT AND INDEPENDENT VECTORSBOOK - CENGAGE PUBLICATIONCHAPTER - LINEAR COMBINATION OF VECTORS, DEPENDENT AND INDEPENDENT VECTORSEXERCISE - DPP 1.2
10 Videos
Similar Questions
The reciprocal of the value of: limn→∞(1−122)(1−132)(1−142)(1−1n2)is
View SolutionLet f:R→R be a positive, increasing function with
limx→∞f(3x)f(x)=1. Then limx→∞f(2x)f(x) is equal to
View SolutionLetf(x)=sin−1(1−{x})×cos−1(1−{x})√2{x}×(1−{x}), where {x} denotes the fractional part of x.
L=limx→0−f(x) is equal to
View SolutionIf y = y(x) is the solution of the differential equation, xdydx+2y=x2 satisfying y(1) = 1, then y(12) is equal to
View SolutionThe number of integral values of p for which (p+1)ˆi−3ˆj+pˆk,pˆi+(p+1)ˆj−3ˆk and −3ˆi+pˆj+(p+1)ˆk are linearly dependent vectors is q
View SolutionFactorise the expressions. (i) ax2+bx
(ii) 7p2+21q2
(iii) 2x3+2xy2+2xz2
(iv) am2+bm2+bn2+an2
(v) (lm+l)+m+1
(vi) y(y+z)+9(y+z)
(vii) 5y2−20y−8z+2yz
(viii) 10ab+4a+5b+2
(ix) 6xy−4y+6−9x
View SolutionABCD is a rectangle. Points M and N are on BD such that AM⊥BD and CN⊥BD . Prove that BM2+BN2=DM2+DN2 .
View SolutionABCD is a rectangle. AM bot BD And CN bot BD Then prove that BM^(2) + BN^(2) = DM^(2) + DN^(2)
View SolutionFactorise the expressions. (i) ax2+bx (ii) 7p2+21q2 (iii) 2x3+2xy2+2xz2 (iv) am2+bm2+bn2+an2 (v) (lm+l)+m+1 (vi) y(y+z)+9(y+z) (vii) 5y2−20y−8z+2yz (viii) 10ab+4a+5b+2 (ix) 6xy−4y+6−9x
View Solutionযদি ma=nb হয়, তবে দেখাই যে, (m2+n2)(a2+b2)=(am+bn)2
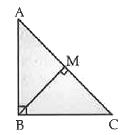
View SolutionIn ΔABC, ∠ABC=90∘, BM⊥AC, AM=8x2,AM=2x2, find BM and AB.
View SolutionFactorize the expressions:am2+bm2+bn2+an2
View Solutionਹੇਠਾ ਲਿਖੇ ਵਿਅੰਜਕਾਂ ਦੇ ਗੁਣਨਖੰਡ ਬਣਾਉ : am2+bm2+bn2+an2
View Solutionगुणनखण्ड निकालें:
am2+bm2+bn2+an2
View Solutionयदि (a2+b2)(m2+n2)=(am+bn)2 तब,
View SolutionThe factorisation of am^2 + bm^2 + bn^2 + an^2 is
View Solution
