At the endpoint and midpoint of a circular are AB, tangent lines are drawn, and the points, A and B are jointed with a chord. Prove that the ratio of the areas of the triangles thus formed tends to 4 as the arc AB decreases infinitely.Solution in Bengali

Let Δ1=Area of triangle ABC
and Δ2=Area of triangle CDE
In AFO,AF=Rsinθ and OF=Rcosθ
MF=OM−OF=R−Rcosθ
In triangle OAC,OC=Rsecθ
∴ CM=OC−OM=Rsecθ−R
∴ CF=CM+MF=Rsecθ−Rcosθ
So, Δ1=12AB.CF
=122Rsinθ.R(secθ−cosθ)
=R2tanθ(1−cos2θ)
In triangle CMD,DM=CMcotθ
=(Rsecθ=−R)cotθ
∴ Δ2=122(Rsecθ−R)cotθ.(Rsecθ−R)
=R2(1−cos2θ)2cos2θ.tanθ
∴ Δ1Δ2=tanθ(1−cos2θ)cos2θtanθ(1−cosθ)2
=sin2θ(1+cosθ)(1−cosθ)
∴ limθ→0Δ1Δ2=limθ→0sin2θ(1+cosθ)(1−cosθ)
=limθ→0sin2θ(1+cosθ)21−cos2θ
=limθ→0(1+cosθ)2=4
Topper's Solved these Questions
- LIMITSBook:CENGAGE PUBLICATIONChapter:LIMITSExercise:EXERCISE 2.1
Explore 10 Videos
- LIMITSBook:CENGAGE PUBLICATIONChapter:LIMITSExercise:EXERCISE 2.2
Explore 7 Videos
- LIMITSBook:CENGAGE PUBLICATIONChapter:LIMITSExercise:Comprehension Type
Explore 4 Videos
- JEE 2019Book:CENGAGE PUBLICATIONChapter:JEE 2019Exercise:Chapter 10
Explore 8 Videos
- LINEAR COMBINATION OF VECTORS, DEPENDENT AND INDEPENDENT VECTORSBook:CENGAGE PUBLICATIONChapter:LINEAR COMBINATION OF VECTORS, DEPENDENT AND INDEPENDENT VECTORSExercise:DPP 1.2
Explore 10 Videos
Similar Questions
Evaluate limx→−2+x2−12x+4.
View SolutionIf |f(x)|≤x2, then prove that limx→0f(x)x=0.
View Solutionlimx→0sin2xx
View SolutionIf y = y(x) is the solution of the differential equation, xdydx+2y=x2 satisfying y(1) = 1, then y(12) is equal to
View SolutionThe number of integral values of p for which (p+1)ˆi−3ˆj+pˆk,pˆi+(p+1)ˆj−3ˆk and −3ˆi+pˆj+(p+1)ˆk are linearly dependent vectors is q
View SolutionAt the endpoint and midpoint of a circular are AB, tangent lines are drawn, and the points, A and B are jointed with a chord. Prove that the ratio of the areas of the triangles thus formed tends to 4 as the arc AB decreases infinitely.
View SolutionLet (a, b) is the midpoint of the chord AB of the circle x^2 + y^2 = r^2. The tangents at A and B meet at C, then the area of triangle ABC
View SolutionPoints A and B are on a circle of radius 5 and AB=6. Point C is the midpoint of the minor arc AB length of the line segement AC, is:
View SolutionAB is a chord of the circle x^(2)+y^(2)=9 .The tangents at A and B intersect at C. If M(1,2) is the midpoint of AB,then the area of triangle ABC is
View Solutionसिद्ध कीजिए कि वृत्त के किसी चाप के मध्य बिन्दु पर खींची गई स्पर्श रेखा, चाप के अन्तः बिन्दुओं को मिलाने वाली जीवा के समान्तर होती हैं।
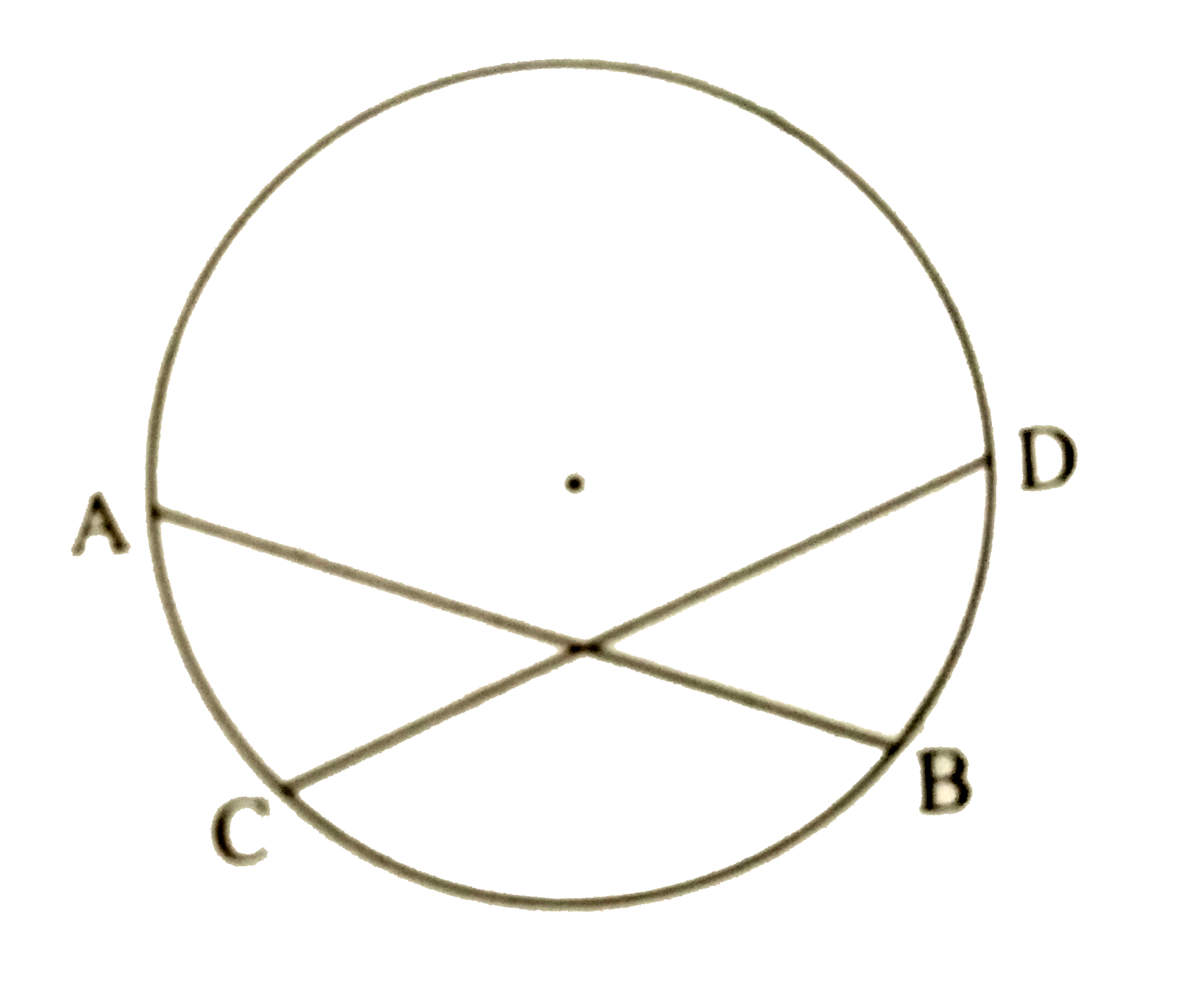
View SolutionIn the figure, chord AB ≅ chord CD
Prove that ,
ar AC ≅ arc BD
View Solutionचित्र में l∣∣m तथा M, रेखाखण्ड AB का मध्य बिंदु है । सिद्ध कीजिए कि M, एक रेखाखण्ड CD, जिसके अन्तः बिंदु l व mपर स्थित है , का भी मध्य बिंदु है ।

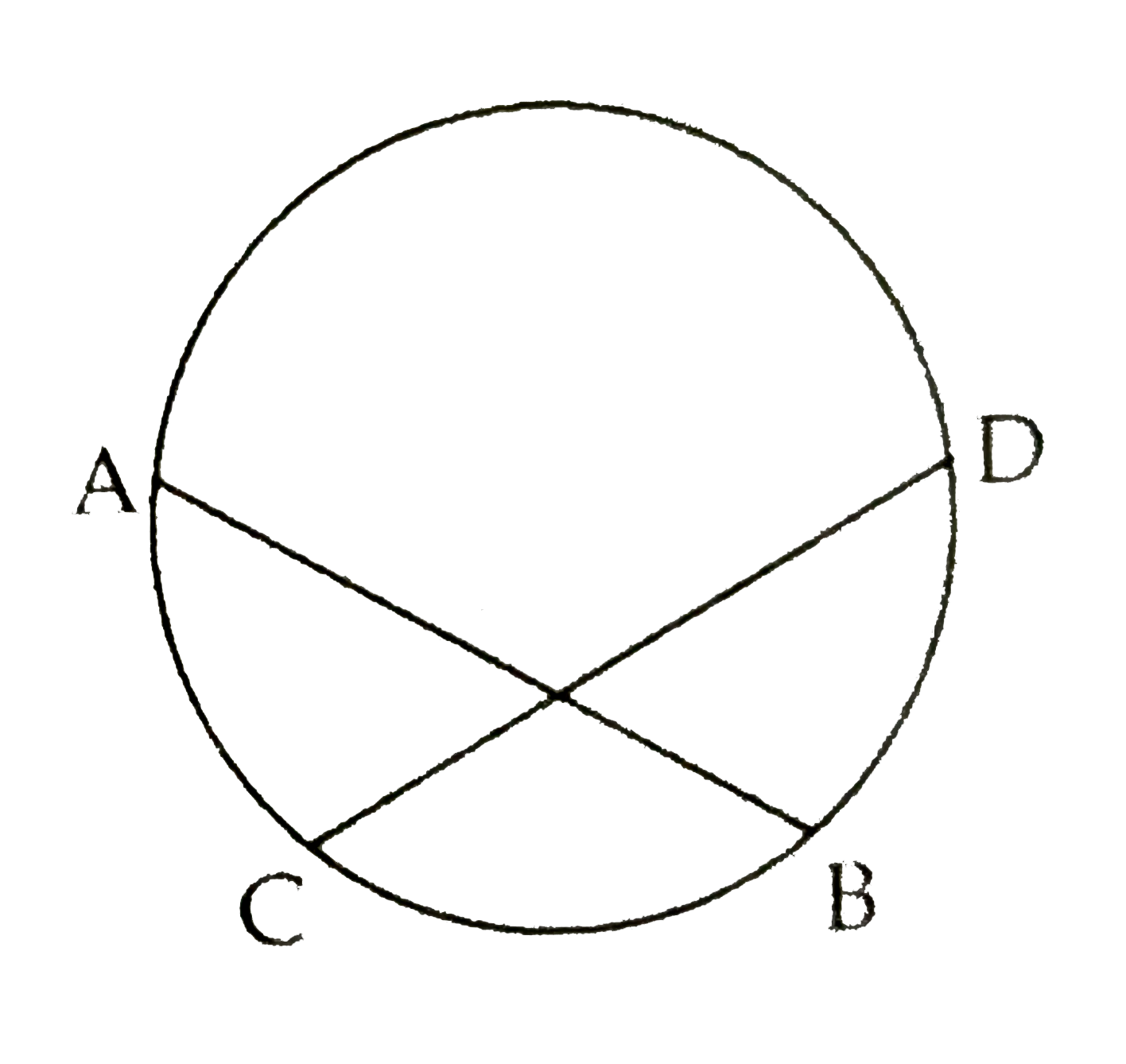
View SolutionIn the adjoining figure, chord AB ≅ chord CD . Prove that arc AC ≅ BD
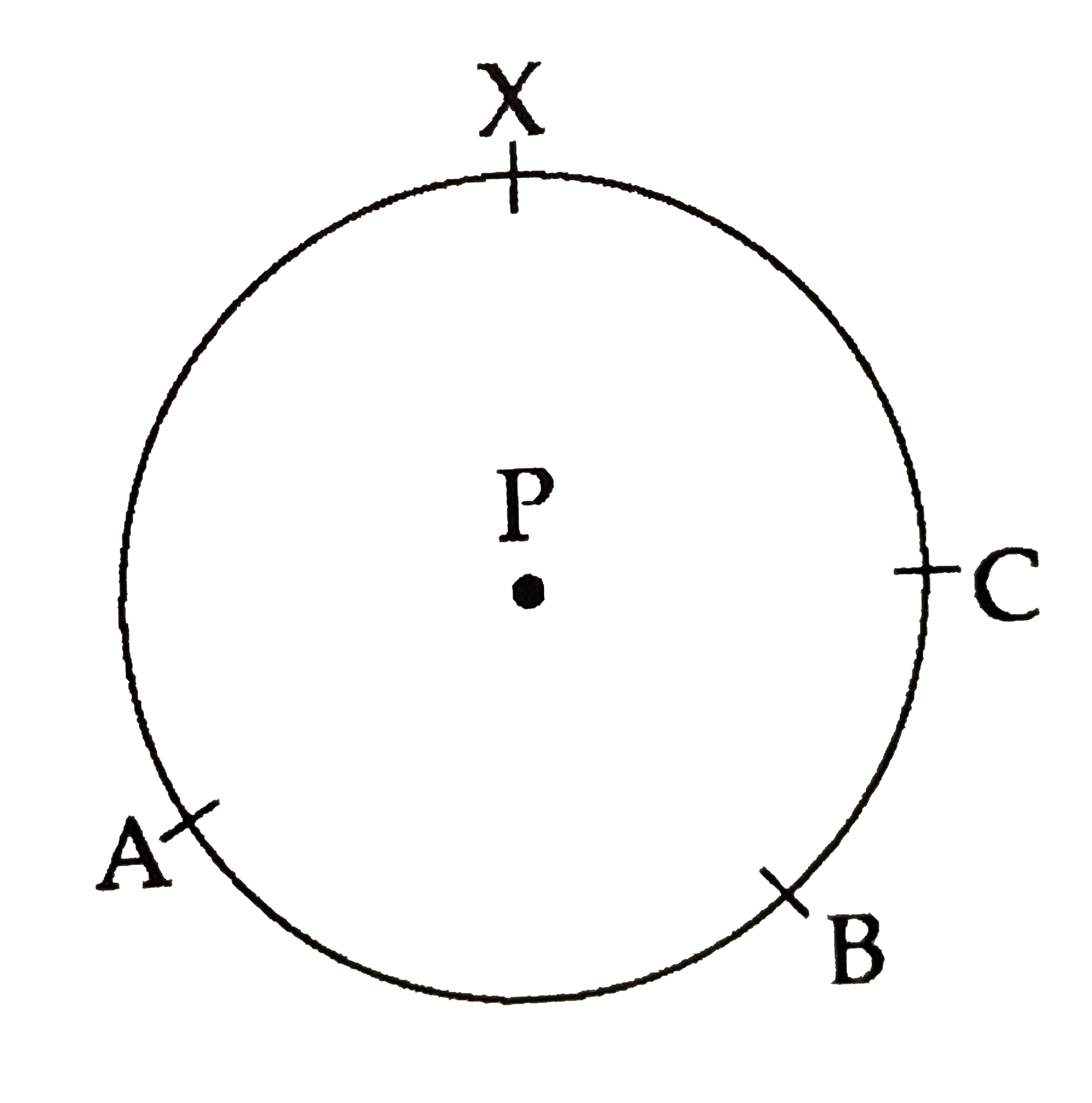
View SolutionA circle with centre P. arc AB = arc BC and arc AXC = 2 arc AB . Find measure of arc AB, arc BC and arc AXC. Prove that chord AB≅ chord BC .
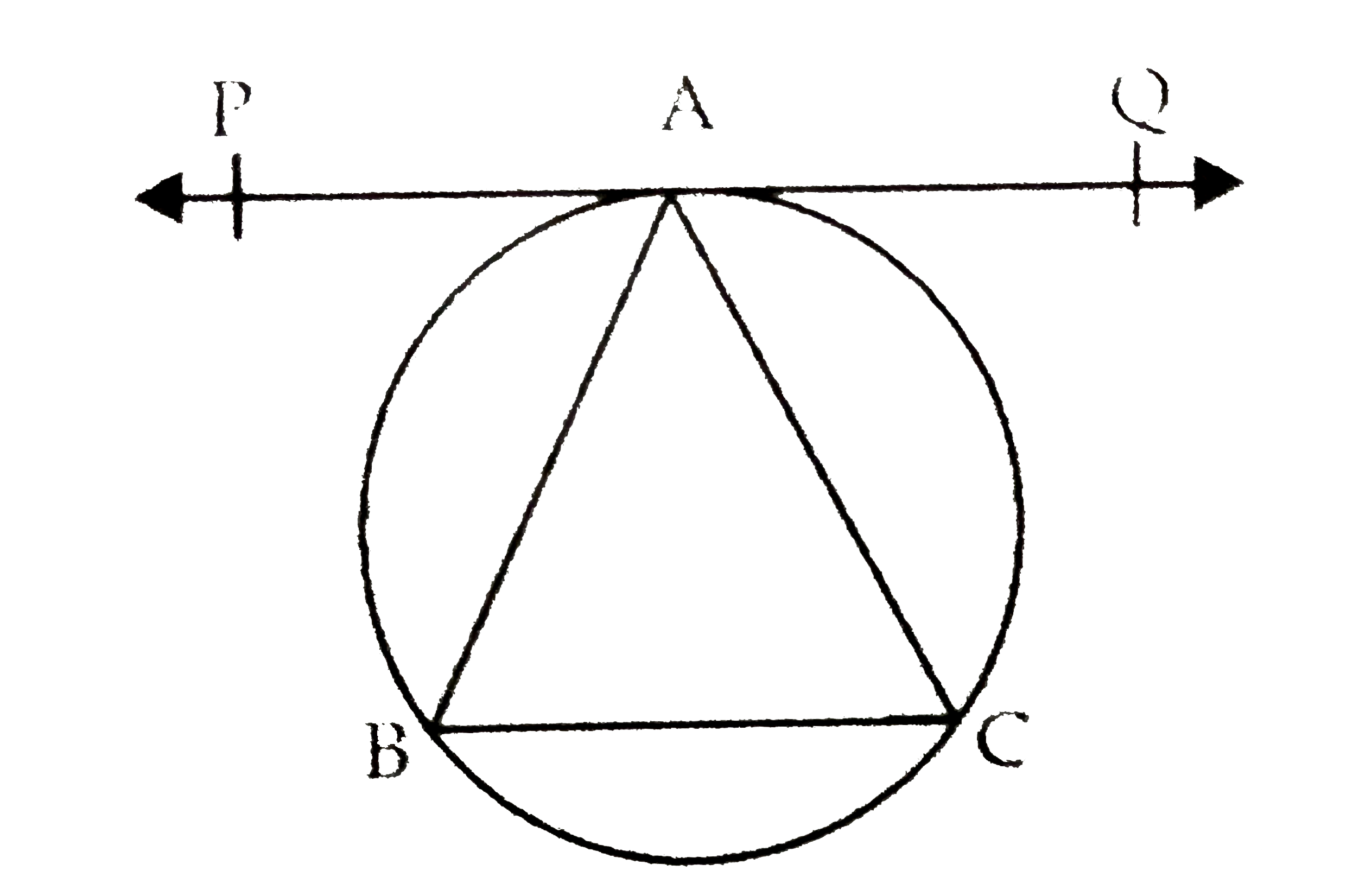
View SolutionLine PQ is a tangent to the circle at point AB ≅ arc AC. Complete the following activity to prove ΔABC as isosceles triangle.
View SolutionFrom the point (4, 6) a pair of tangent lines are drawn to the parabola, y2=8x. The area of the triangle formed by these pair of tangent lines & the chord of contact of the point (4, 6) is
View Solution