Question

$\underset{x\to c}{lim}f\left(x\right)$ does not exist for
wher $[.]$ represent greatest integer function $\{.\}$ represent fractional part function

Explanation

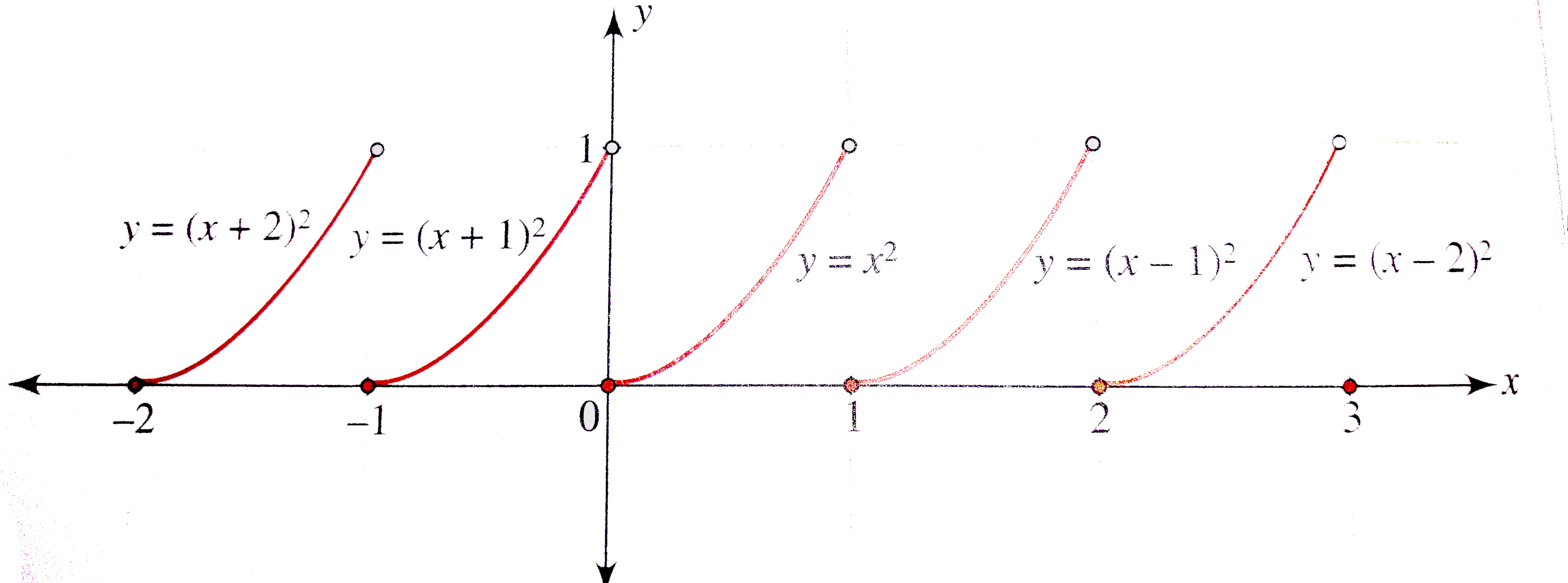
We have `y= f(x) = {x}^(2)`
or `" "y= (x-[x])^(2)`
Since `0 le {x} lt 1, 0 le {x}^(2) lt 1`.
For `0le x lt 1, y = x^(2)`, which is a half parabola to the right of the vertex at `(0, 0)`.
For `1 le x lt 2, y = (x-1)^(2)`, which is a half parabola to the right of the vertex at (1, 0).
For `2 le x lt 3, y = (x+1)^(2)`, which is a half parabola to the right of the vertex at (2, 0).
For ` -1 le x lt 0, y= (x+1)^(2)`, which is a half parabola to the right of the vertex at `(-1, 0)`, and so on.
The graph of the function is as shown in the following figure.