Question

Draw the graph of the function $y=3x^4-4x^3$. Discuss the points of local extremum, inflection and intervals of monotonicity.

Explanation

We have `y=f(x)=3x^(4)-4x^(3)=x^(3)(3x-4)`
The sign scheme of `y=f(x)` is as follows.

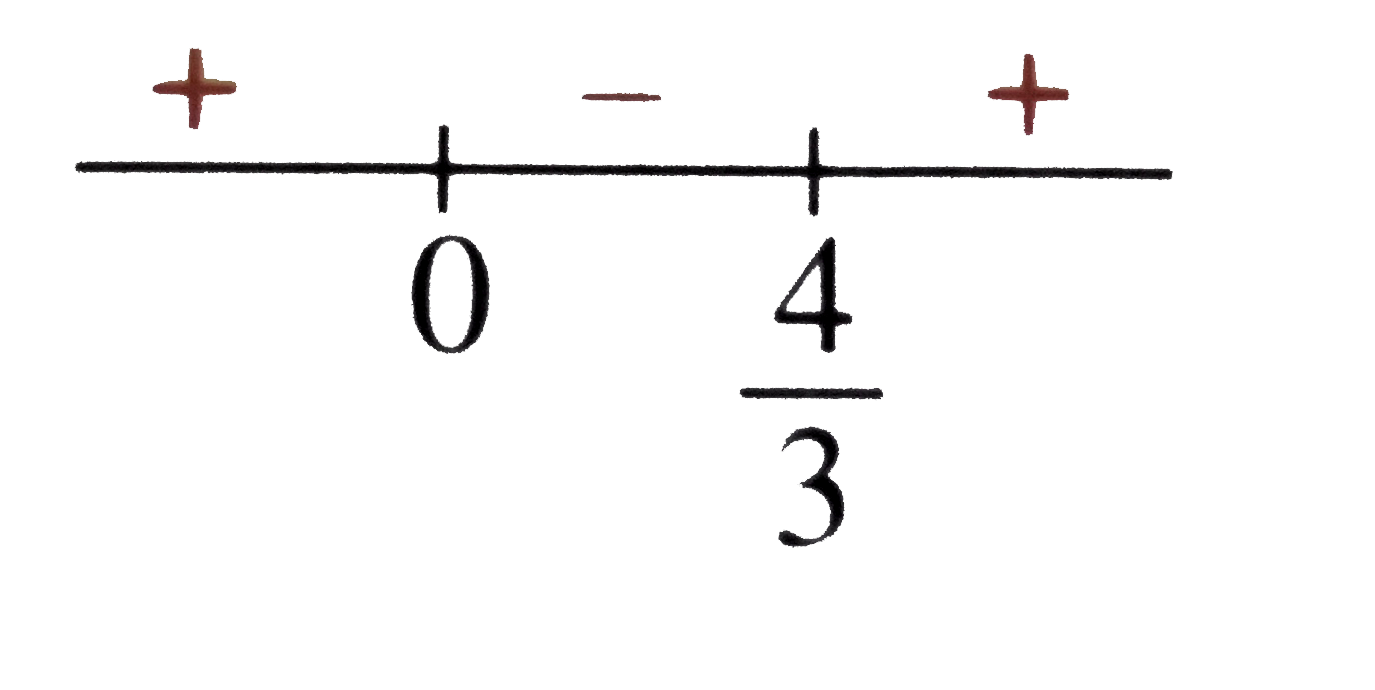
`(3x-4)rarr` Graph crosses the x-axis at `x=4//3` without touching the x-axis.
`x^(2)rarr` Graph crosses the x-axis at (0,0) and also touches the x-axis at this point.
`f'(x)=12x^(3)-12x^(2)`
`=12x^(2)(x-1)`
`f'(x)=0`
`:. " " x=0, 1`
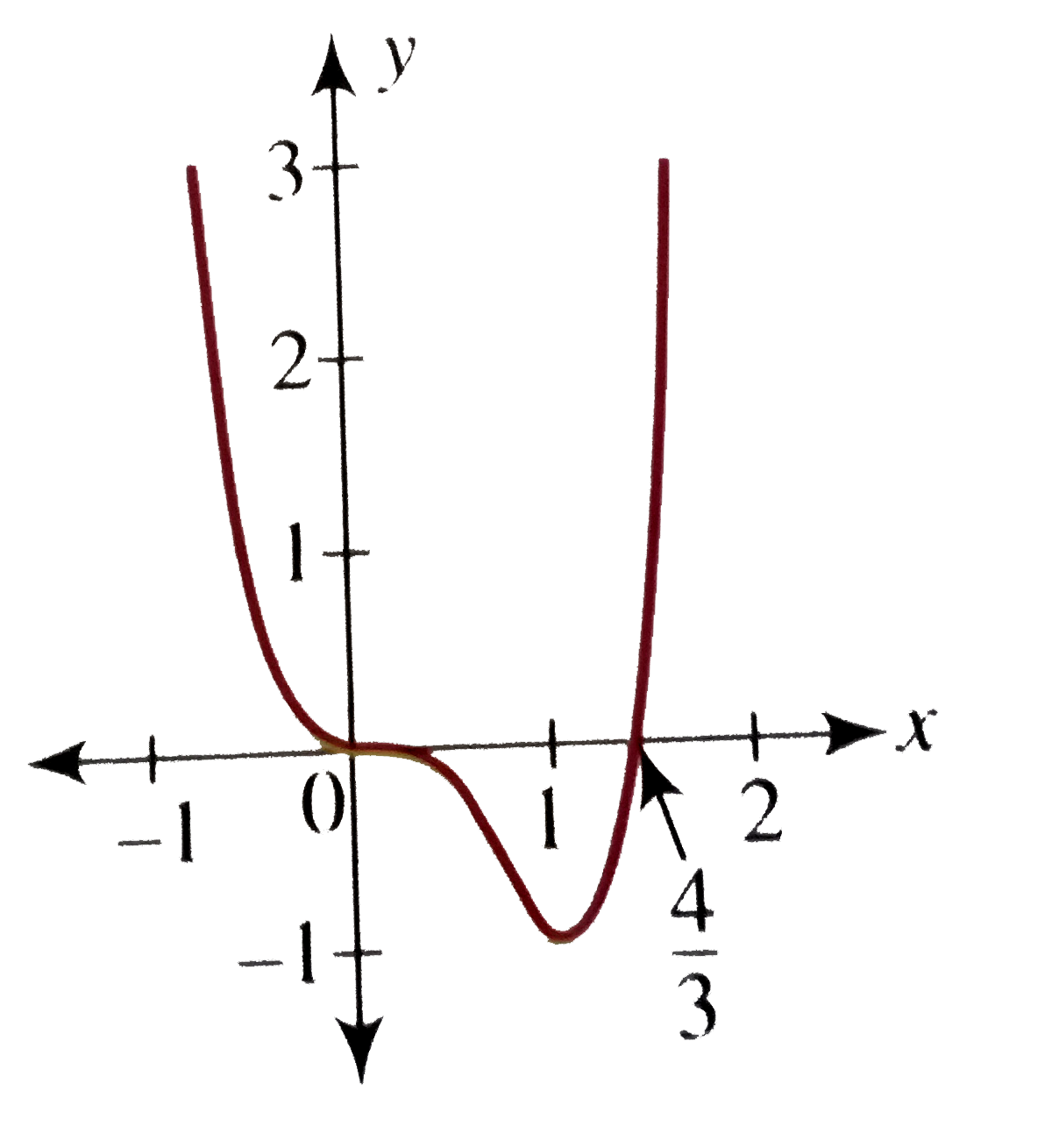
`f'(x) lt 0, "if " x lt 1`, where `f(x)` decreases
`f'(x) gt0, "if " x gt1`, where `f(x)` increases
`x=1` is the point of minima.
Also `f''(x)=36x^(2)-24x=12x(3x-2)`
`f''(x)=0, "if " x=0, 2//3`, which are points of inflection .
The graph of the function is as shown in the following figure.