PQ is a vertical tower having P as the foot. A,B,C are three points in the horizontal plane through P. The angles of elevation of Q from A,B,C are equal and each is equal to θ . The sides of the triangle ABC are a,b,c, and area of the triangle ABC is △ . Then prove that the height of the tower is (abc) tanθ4'△'.Solution in Bengali
Let the height of the tower PQ be h.
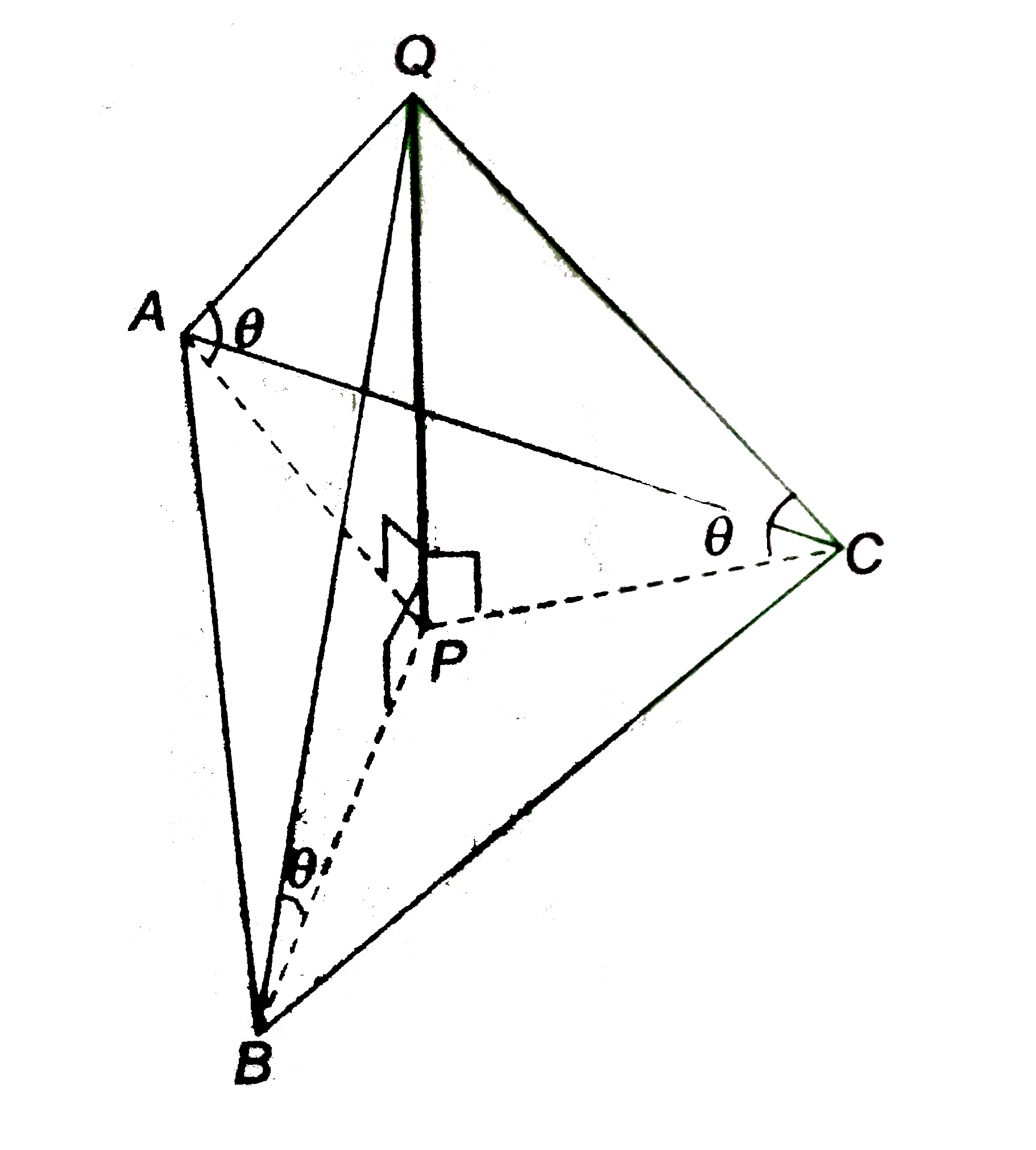
AP = BP =CP =hcotθ
Therefore , P is the circumcentre of ΔABC
∴AP=BP=CP=R=abc4Δ
∴h=abc4Δtanθ
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - HIGHT AND DISTANCE EXERCISE - Exercises18videos
HIGHT AND DISTANCE
- BOOK - CENGAGE PUBLICATIONCHAPTER - HIGHT AND DISTANCE EXERCISE - Archives3videos
HIGHT AND DISTANCE
- BOOK - CENGAGE PUBLICATIONCHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercises22videos
GRAPHS OF TRIGONOMETRIC FUNCTIONS
- BOOK - CENGAGE PUBLICATIONCHAPTER - HYPERBOLAEXERCISE - COMPREHENSION TYPE2videos
HYPERBOLA
Similar Questions
The tops of two poles of height 20 m and 14 m are connected by a wire. If the wire makes an angle of 30o with horizontal, then the length of the wire is (a) 12 m (b) 10 m (c) 8 m (d) 6 m
02:41View SolutionA bird is sitting on the top of a vertical pole 20 m high and its elevation from a point O on the ground is 45o . It flies off horizontally straight away from the point O. After one second, the elevation of the bird from O is reduced to 30o . Then the speed (in m/s) of the bird is (1) 40(√2−1) (2) 40(√3−2) (3) 20√2 (4) 20(√3−1)
02:11View SolutionDraw the graph of y= cosec 2x−cot2x. Is f(x) periodic ? If yes, what is its fundamental period ?
02:36View SolutionThe circle x2+y2−8x=0 and hyperbola x29−y24=1 I intersect at the points A and B. Equation of a common tangent with positive slope to the circle as well as to the hyperbola is (A) 2x−√5y−20=0 (B) 2x−√5y+4=0 (C) 3x−4y+8=0 (D) 4x−3y+4=0
View SolutionPQ is a vertical tower having P as the foot. A,B,C are three points in the horizontal plane through P. The angles of elevation of Q from A,B,C are equal and each is equal to θ . The sides of the triangle ABC are a,b,c, and area of the triangle ABC is . Then prove that the height of the tower is (abc) tanθ4.
03:21View SolutionAngle A, B, C of a triangle ABC are equal to each other. Prove that ABC is equilateral.
05:02View SolutionThe angle of elevation of the top of the tower observed from each of three points A,B , C on the ground, forming a triangle is the same angle α. If R is the circum-radius of the triangle ABC, then find the height of the tower
03:21View SolutionIn a triangle ABC, IF angle B is twice angle C then c (b +a) is equal to
05:18View SolutionThe angle of elevation of the top of the tower observed from each of the three points A,B,C on the ground, forming a triangle is the same anlge alpha . IF R is the circumradius of the Delta ABC , then the height of the tower is
View Solutionएक ऊर्ध्वाधर मीनार PQ है | मीनार का पद P तथा शीर्ष Q है | A, B, C, P से जाने वाले क्षैतिज तल पर तीन बिन्दु है | बिन्दु A, B, C से Q के उन्नयन कोण समान है तथा के बराबर है | की भुजाएँ a, b व c क्षेत्रफल Δ है | दिखाइए कि मीनार की ऊँचाई abctanθ4Δ है |
05:25View SolutionABC is a vertical tower such that AB=BC=x from the foot A of the tower a horizontal line AQP is drawn.If the angle of elevation of the point B from P is α and that of C from Q is 2α then (AP)(PQ) is equal to
02:27View Solutionधरातल पर त्रिभुज बनाने वाले तीन बिंदुओं A,B,C में से प्रत्येक का किसी टॉवर के शिखर पर उन्नयन कोण α है। यदि R,ΔABC की परित्रिज्या हो, तो टॉवर की ऊंचाई है
04:16View SolutionA vertical tower CP subtends the same angle θ, at point B on the horizontal plane through C, the foot of the tower, and at point A in the vertical plane. If the triangle ABC is equilateral with length of each side equal to 4 m, the height of the tower is
02:31View SolutionPQ is a vertical tower having P as the foot. A,B,C are three points in the horizontal plane through P. The angles of elevation of Q from A,B,C are equal and each is equal to θ . The sides of the triangle ABC are a,b,c, and area of the triangle ABC is △ . Then prove that the height of the tower is (abc) tanθ4'△'.
02:11View SolutionPQ is a vertical tower having P as the foot. A,B,C are three points in the horizontal plane through P. The angles of elevation of Q from A,B,C are equal and each is equal to θ . The sides of the triangle ABC are a,b,c, and area of the triangle ABC is . Then prove that the height of the tower is (abc) tanθ4.
03:07View Solutionएक मीनार के सिरे का भुमि पर त्रिभुज बनाने वाले तीन बिन्दुओं A,B,C में से प्रत्येक से उन्यन कोण समान तथा α के बराबर है यदि त्रिभुज ABC के परित्रिज्या R हैं तब मीनार की ऊँचाई है
02:31View Solution