Find the asymptote of the function y=2x2+3x+1x if any.Solution in Bengali
Vertical asymptote:
Since denominator is x, vertical asymptote is x = 0.
Oblique asymptote:
Let the oblique asymptote by y = mx + n. Therefore,
limx→∞[2x2+3x+1x−(mx+n)]=0
⇒limx→∞[2x2+3x+1−(mx+n)xx]=0
⇒limx→∞[(2−m)x2+(3−n)x+1x]=0
Clearly, 2 - m = 0
⇒limx→∞[(3−n)x+1x]=0
⇒limx→∞[(3−n)+1x]=0
⇒3−n=0
⇒n=3
Thus, the oblique asymptote is y = 2x + 3.
Alternative method:
We have 2x2+3x+1x=2x+3+1x
Here quotient is 2x+3, hence the oblique asymptote is y = 2x +3.
Topper's Solved these Questions
- GETTING STARTED WITH GRAPHSBOOK - CENGAGE PUBLICATIONCHAPTER - GETTING STARTED WITH GRAPHSEXERCISE - ILLUSTRATION 1.28
1 Videos
- GETTING STARTED WITH GRAPHSBOOK - CENGAGE PUBLICATIONCHAPTER - GETTING STARTED WITH GRAPHSEXERCISE - Exercises 1.1
1 Videos
- GETTING STARTED WITH GRAPHSBOOK - CENGAGE PUBLICATIONCHAPTER - GETTING STARTED WITH GRAPHSEXERCISE - ILLUSTRATION 1.26
1 Videos
- FUNCTIONSBOOK - CENGAGE PUBLICATIONCHAPTER - FUNCTIONSEXERCISE - Comprehension Type
7 Videos
- GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONSBOOK - CENGAGE PUBLICATIONCHAPTER - GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercises
18 Videos
Similar Questions
Find the horizontal, vertical and oblique asymptotes of each of the curves.
(a)y=xx+4(b)y=x2+4x2−1(c)y=x3x2+3x−10(d)y=x3+1x3+x(e)y=x4√x4+1(f)y=x−9√4x2+3x+2(g)y=12x−1(h)y=1logex(i)y=12x+1
View Solution
Does the following graph pass the vertical or horizontal line test ?

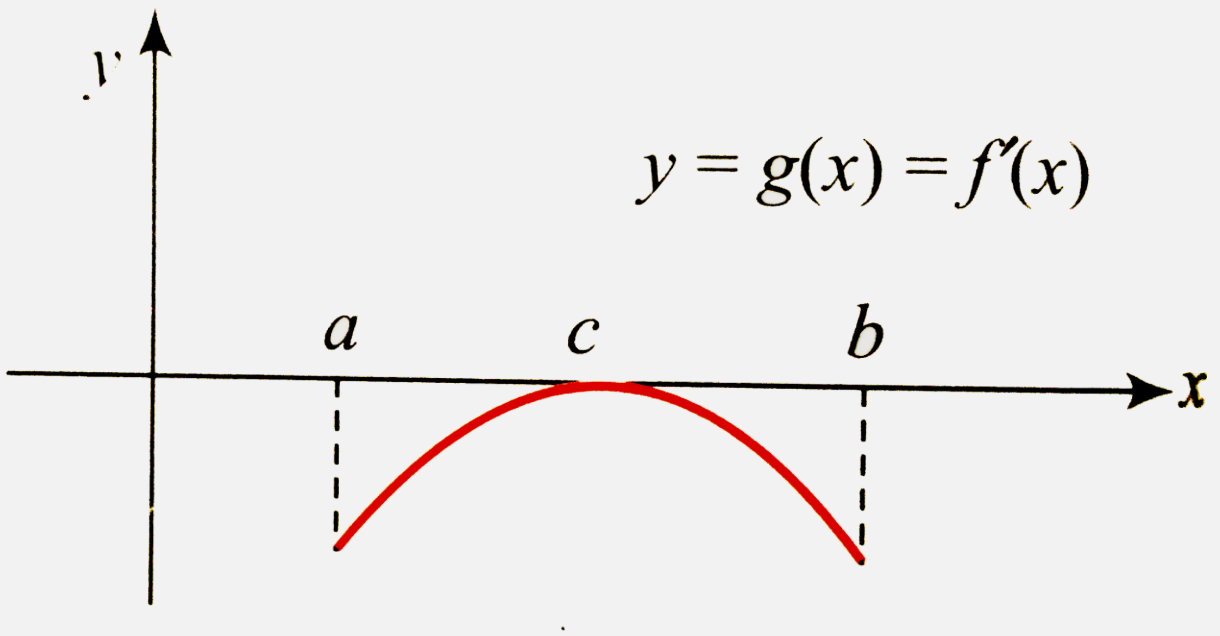
View SolutionFollowing is the graph of y = f' (x) , given that f(c) = 0. Analyse the graph and answer the following questions.
(a) How many times the graph of y = f(x) will intersect the x - axis?
(b) Discuss the type of roots of the equation f (x) = 0, a≤x≤b.
(c) How many points of inflection the graph of y=f(x),a≤x≤b, has?
,(d) Find the points of local maxima/minima of y=f(x),a≤x≤b,
, (e) f"(x)=0 has how many roots?
View SolutionLet f(x)=x2−2x−1∀x∈R.Letf:(−∞,a]→[b,∞), where a is the largest real number for which f(x) is bijective.
If f:R→R, then range of values of k for which equation f(|x|)=k has 4 distinct real roots is
View SolutionDraw the graph of y=tan−1x−cot−1x.
View SolutionFind the asymptotes of the following curves: y3−3x2y+xy2−3x3+2y2+2xy+4x+5y+6=0
View SolutionThe line x+y+1=0 is an asymptote of x2−y2+x−y−2=0. The other asymptote is
View SolutionFind the asymptote of the function y=2x2+3x+1x if any.
View SolutionFind the equation of a hyperbola whose asymptotes are 2x−y−3=0and3x+y−7=0 and which pass through (1,1).
View SolutionFind the prodcut of lengths from any point on the hyperbola x216−y29=1 to its asymptotes.
View SolutionWhich of the following is the equation of an asymptote of y=3x2−2x−19x2−1 ?
View SolutionWhich of the following is horizontal asymptote to the function f(x)=3x4−7x3+2x2+12x4−4 ?
View SolutionFind the slant (oblique) asymptote of the function f(x)=x2+3x+5x+2
View SolutionFind the asymptotes of the function f(x)=1x
View SolutionFind the asymptotes x3−2x2y−2x2+4xy−4y2+4x+y+3=0
View SolutionThe line x+y+1=0 is an asymptote of x2−y2+x−y−2=0. The other asymptote is
View Solution
