let L be a straight line passing through the origin. Suppose that all the points on L are at a constant distance from the two planes P1:x+2y−z+1=0 and P2:2x−y+z−1=0, Let M be the locus of the feet of the perpendiculars drawn from the points on L to the plane P1. Which of the following points lie(s) on M? (a) (0,−56,−23) (b) (−16,−13,16) (c) (−56,0,16) (d) (−13,0,23)Solution in Bengali
(0,−56,−23)
(−16,−13,16)
(−56,0,16)
(−13,0,23)
The correct Answer is:A, B
a.b .
Let →v be the vetor along I.
P1:x+2y−Z+1=0andP2:2x−y+z−1=0
∴→c=∣∣(ˆi,ˆj,ˆk),(1,2,−1),(2,−1,1)}∣∣=ˆi−3ˆj−5ˆk
since I. is through origin any point on line I. is A(λ,3λ,−5λ).Foot of perpendicular from A to P1 , is
h−λ1=(k+3lamda)/(-1)=-(lamda-6lamda+5lamda+1))/(1+4+1)=-(1)/(6)<br>therefore h= lammda-(1)/(6) ,k =- 3lamda -(1)/(3) ,il=-5 lamda+(1)/(6)<br>so,f∞trorp∮onlovusMis(lamda-(1)/(6),-3lamda-(1)/(3)-(1)/(3),-5lamda+(1)/(6))
So points (a) and (b) lie on this loucs .
Topper's Solved these Questions
- JEE 2019BOOK - CENGAGE PUBLICATIONCHAPTER - JEE 2019EXERCISE - chapter-2
1 Videos
- JEE 2019BOOK - CENGAGE PUBLICATIONCHAPTER - JEE 2019EXERCISE - single correct answer type
1 Videos
- JEE 2019BOOK - CENGAGE PUBLICATIONCHAPTER - JEE 2019EXERCISE - matching column type
2 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBOOK - CENGAGE PUBLICATIONCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - All Questions
541 Videos
- LIMITSBOOK - CENGAGE PUBLICATIONCHAPTER - LIMITSEXERCISE - Comprehension Type
4 Videos
Similar Questions
Let →u=u1ˆi+u2ˆj+u3ˆk be a unit vector in R3and→w=1√6(ˆi+ˆj+2ˆk) , Given that there exists a vector →v in R3 such that |→u×→v|=1and→w.(→u×→v)=1 which of the following statements is/are correct ?
View Solutionthe mirror image of point (3,1,7) with respect to the plane x−y+z=3 is P. then equation plane which is passes through the point P and contains the line x1=y2=z1.
View Solution
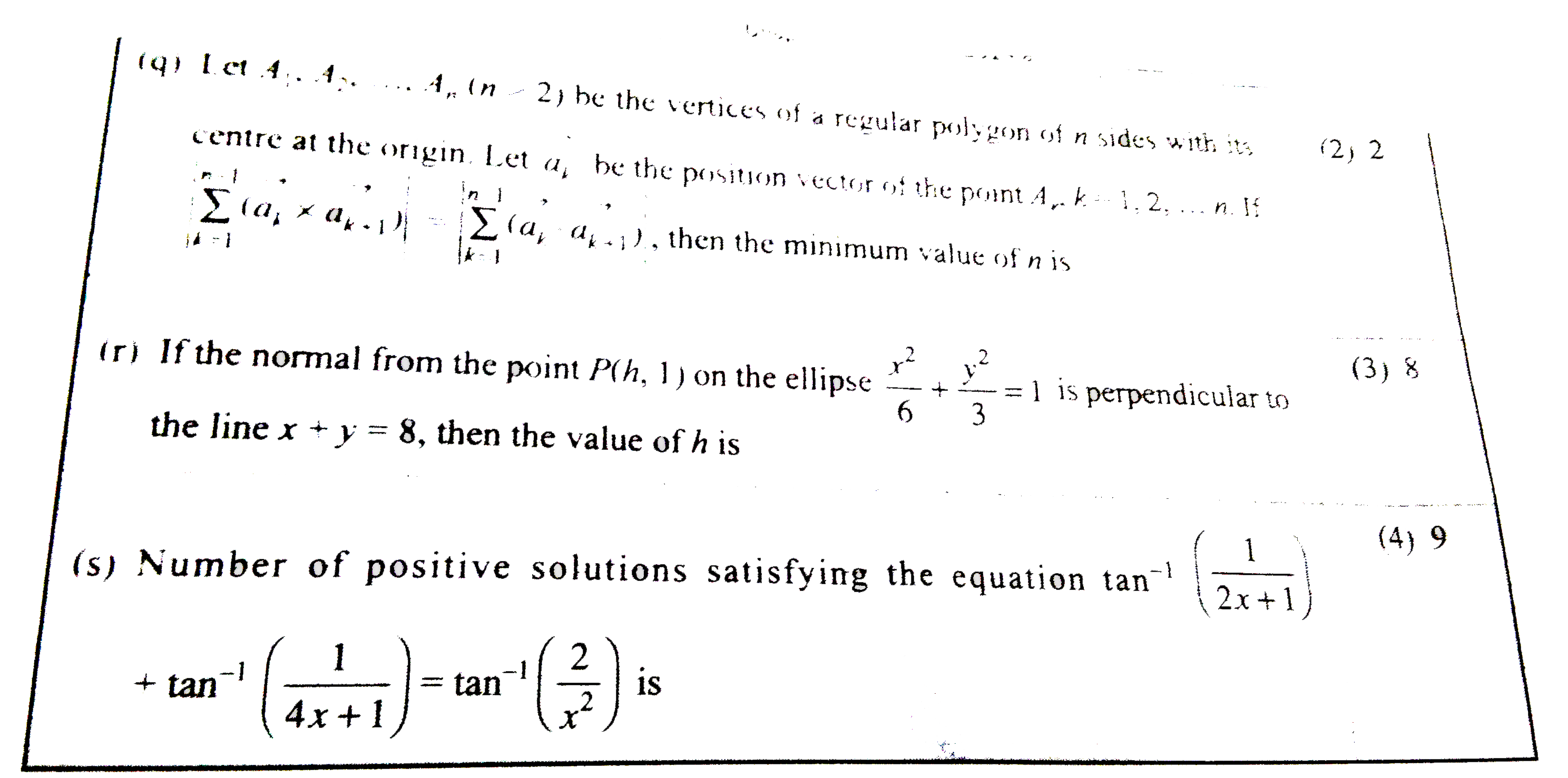
View SolutionFind x satisfying [tanx]+[cotx]=2, where [.] represents the greatest integer function.
View Solutionlimx→0sin2xx
View SolutionIn R', consider the planes P1,y=0 and P2:x+z=1. Let P3, be a plane, different from P1, and P2, which passes through the intersection of P1, and _2P If the distance of the point (0,1,0) from P3, is 1 and the distance of a point (α,β,γ) from P3 is 2, then which of the following relation is (are) true ?
View SolutionIn R', consider the planes P1,y=0 and P2:x+z=1. Let P3, be a plane, different from P1, and P2, which passes through the intersection of P1, and P2. If the distance of the point (0,1,0) from P3, is 1 and the distance of a point (α,β,γ) from P3 is 2, then which of the following relation is (are) true ?
View Solutionlet L be a straight line passing through the origin. Suppose that all the points on L are at a constant distance from the two planes P1:x+2y−z+1=0 and P2:2x−y+z−1=0, Let M be the locus of the feet of the perpendiculars drawn from the points on L to the plane P1. Which of the following points lie(s) on M?
View SolutionLet P1:2x+y−z=3 and P2:x+2y+z=2 be two planes. Then, which of the following statement(s) is (are) TRUE? The line of intersection of P1 and P2 has direction ratios 1, 2, −1 (b) The line 3x−49=1−3y9=z3 is perpendicular to the line of intersection of P1 and P2 (c) The acute angle between P1 and P2 is 60o (d) If P3 is the plane passing through the point (4, 2, −2) and perpendicular to the line of intersection of P1 and P2 , then the distance of the point (2, 1, 1) from the plane P3 is 2√3
View SolutionConsider the planes p1:2x+y+z+4=0,p2:y−z+4=0andp3:3x+2y+z+8=0
Let L1,L2,L3 be the lines of intersection of the planes p2andp3,p3andp1,p1andp2 respectively. Then.
View SolutionIn R2, L be a straight line passing through the origin. Suppose that all the points on L are at a constant distance from the two planesp1:x+2y−z+1=0andp2:2x−y+z−1=0. Let M be the locus of the feet of the perpendiculars drawn from the points on L to the plane p1.
Which of the following points lie (s) on M ?
View SolutionIn R3, let L be a straight line passing through the origin. Suppose that all the points on L are at a constant distance from the two planes P1:x+2y−z+1=0andP2:2x−y+z−1=0. Let M be the locus of the feet of the perpendiculars drawn from the points on L to the plane P1. Which of the following points lie (s) on M ?
View Solutionमाना कि R3 में L एक सरल रेखा है जोकि मूल बिंदु से जाती है। माना कि L के सभी बिंदु समतलों P1:x+2y−z−1=0 तथा P2:2x−y+z−1=0 से स्थिर दूरी पर है । माना कि L के बिंदुओं से समतल P1 पर डाले गये लंबों के पादों का पथ M है। निम्नलिखित बिंदुओं में से कौन सा बिंदु पथ M पर स्थित है?
View SolutionR3-তে মূলবিন্দুগামী একটি সরলরেখা হল L। 1. সরলরেখাটি P1:x+2y−z+1=0 এবং P2:2x–y+z–1=0 সমতল দুটি থেকে সমদূরবর্তী। L-এর যে-কোনো বিন্দু থেকে P1,সমতলের উপর অঙ্গিকত লম্বের পাদবিন্দুর সঞ্চারপথ M । নীচের কোন বিন্দু/বিন্দগুলি M -এর ওপর অবস্থিত?
View Solutionlet L be a straight line passing through the origin. Suppose that all the points on L are at a constant distance from the two planes P1:x+2y−z+1=0 and P2:2x−y+z−1=0, Let M be the locus of the feet of the perpendiculars drawn from the points on L to the plane P1. Which of the following points lie(s) on M? (a) (0,−56,−23) (b) (−16,−13,16) (c) (−56,0,16) (d) (−13,0,23)
View Solutionlet L be a straight line passing through the origin. Suppose that all the points on L are at a constant distance from the two planes P1:x+2y−z+1=0 and P2:2x−y+z−1=0, Let M be the locus of the feet of the perpendiculars drawn from the points on L to the plane P1. Which of the following points lie(s) on M?
View Solution
