Match the following Column I to Column II
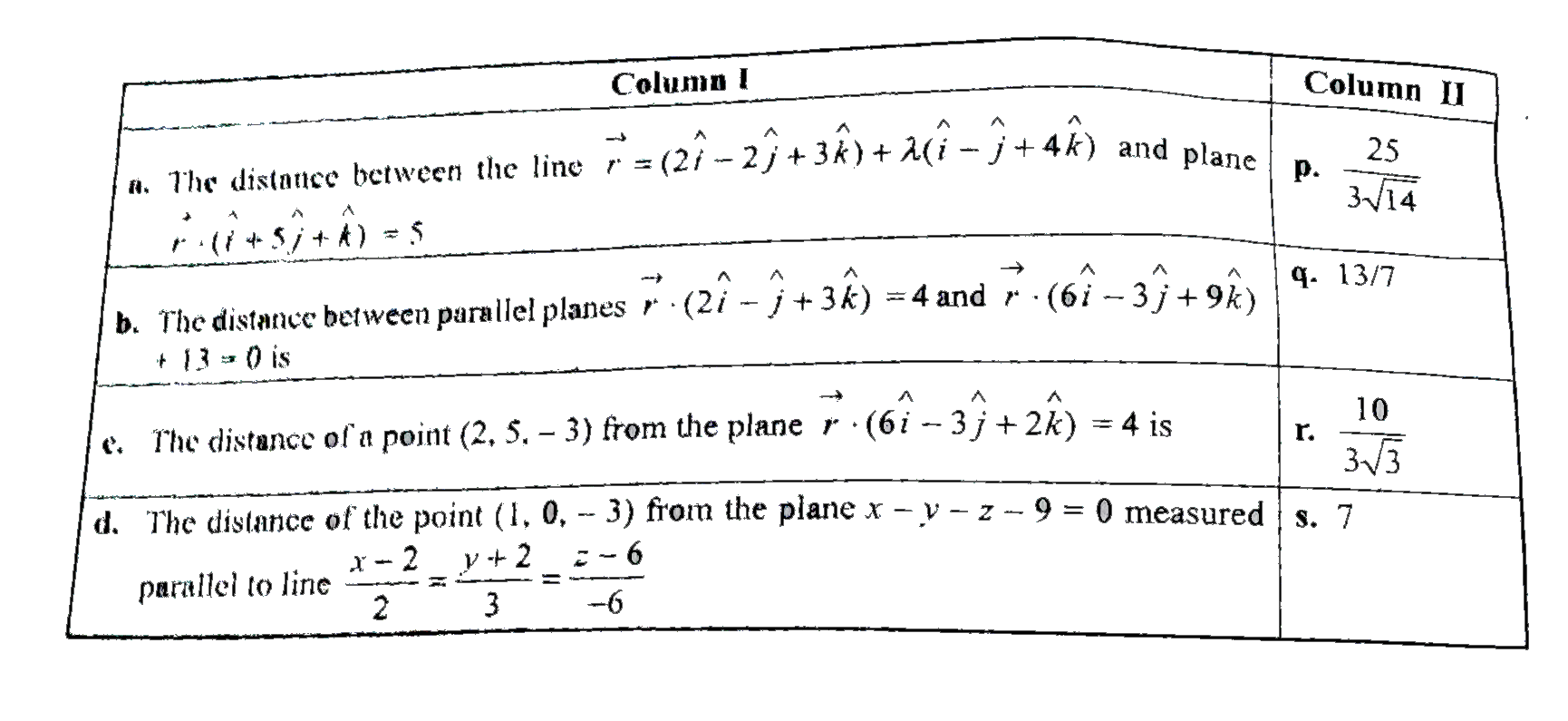Solution in Bengali

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $a \to r; b \to p; c \to q; d \to s$

The given line and plane are $\to r = (2 ˆ i - 2 ˆ j + 3 ˆ k) + λ (ˆ i - ˆ j + 4 ˆ k) and \to r \cdot (ˆ i + 5 ˆ j + ˆ k) = 5$ , respectively. Since $(ˆ i - ˆ j + 4 ˆ k) \cdot (ˆ i + 5 ˆ j + ˆ k) = 0$ , line and plane are parallel.
Hence, the required distance is equal to distance of point $(2, - 2, 3)$ from the plane $x + 5 y + z - 5 = 0$ , which is $\frac{| 2 - 10 + 3 - 5 |}{\sqrt{1 + 25 + 1}} = \frac{10}{3 \sqrt{3}}$
b. The distance between two parallel planes $\to r \cdot (2 i - j + 3 k) = 4 and \to r \cdot (6 i - 3 j + 9 k) + 13 = 0$ is
$d = \frac{| 4 - (- 13 / 3) |}{\sqrt{{(2)}^{2} + {(- 1)}^{2} + {(3)}^{2}}} = \frac{(25 / 3)}{\sqrt{14}}$
$= \frac{25}{3 \sqrt{14}}$
c. The perpendicular distance of the point $(2, 5, - 3)$ fromt the plane $\to r \cdot (6 i - 3 j + 2 k) = 4 or 6 x - 3 y + 2 z - 4 = 0$ is
$d = \frac{| 12 - 15 - 6 - 4 |}{\sqrt{36 + 9 + 4}}$
$= 13 / \sqrt{49} = 13 / 7$
d. The equation of the line $A B$ is
$\frac{x - 2}{2} = \frac{y + 2}{3} = \frac{z - 6}{- 6}$
The equation of line passing through $(1, 0, - 3)$ and parallel to $A B$ is
$\frac{x - 1}{2} = \frac{y}{3} = \frac{z + 3}{- 6} = r$ (say)

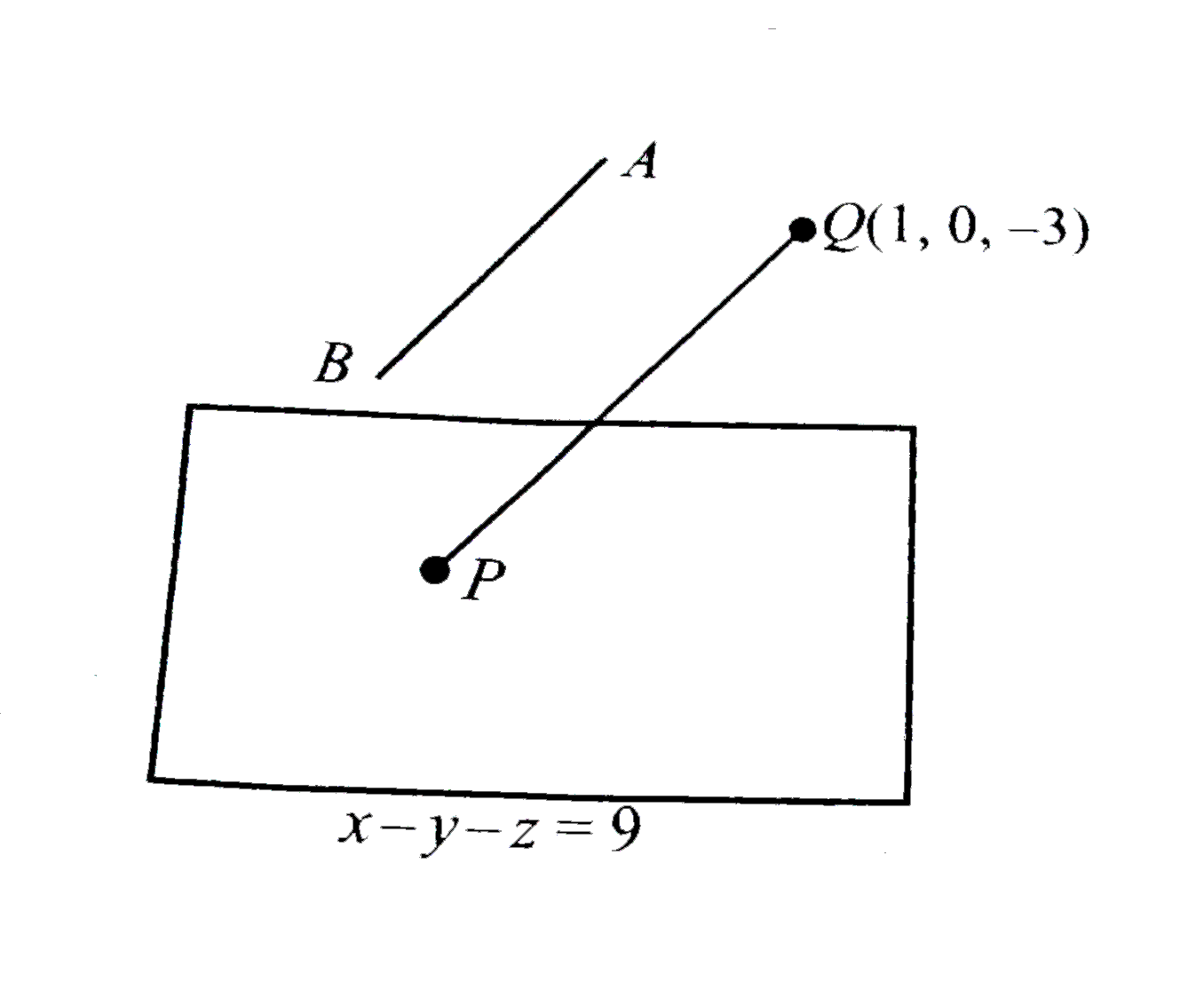
The coordinates of any point on line $P (2 r + 1, 3 r, - 6 r - 3)$ which lie on plane
$(2 r + 1) - (3 r) - (- 6 r - 3) = 9$
$r = 1$
Point $P \equiv (3, 3, - 9)$
Required distance
$P Q = \sqrt{{(3 - 1)}^{2} + {(3 - 0)}^{2} + {(- 9 + 3)}^{2}}$
$= \sqrt{4 = 9 + 36} = 7$

Updated on:21/07/2023

|

Class 12 MATHS THREE DIMENSIONAL GEOMETRY

Topper's Solved these Questions

Similar Questions

CENGAGE PUBLICATION-THREE-DIMENSIONAL GEOMETRY -MATRIX-MATCH TYPE

Home
Ask Doubt
Profile