The number of solutions of 2cosx=|sinx|,0≤x≤4π, is (a) 0 (b) 2 (c) 4 (d) infiniteSolution in Bengali
To find the number of solutions to the equation 2cosx=|sinx|,0≤x≤4π, we need to find how many times the graphs of y=2cosxandy=|sinx| intersect in [0,4π].
The graphs of y=2cosxandy=|sinx| are plotted as ss
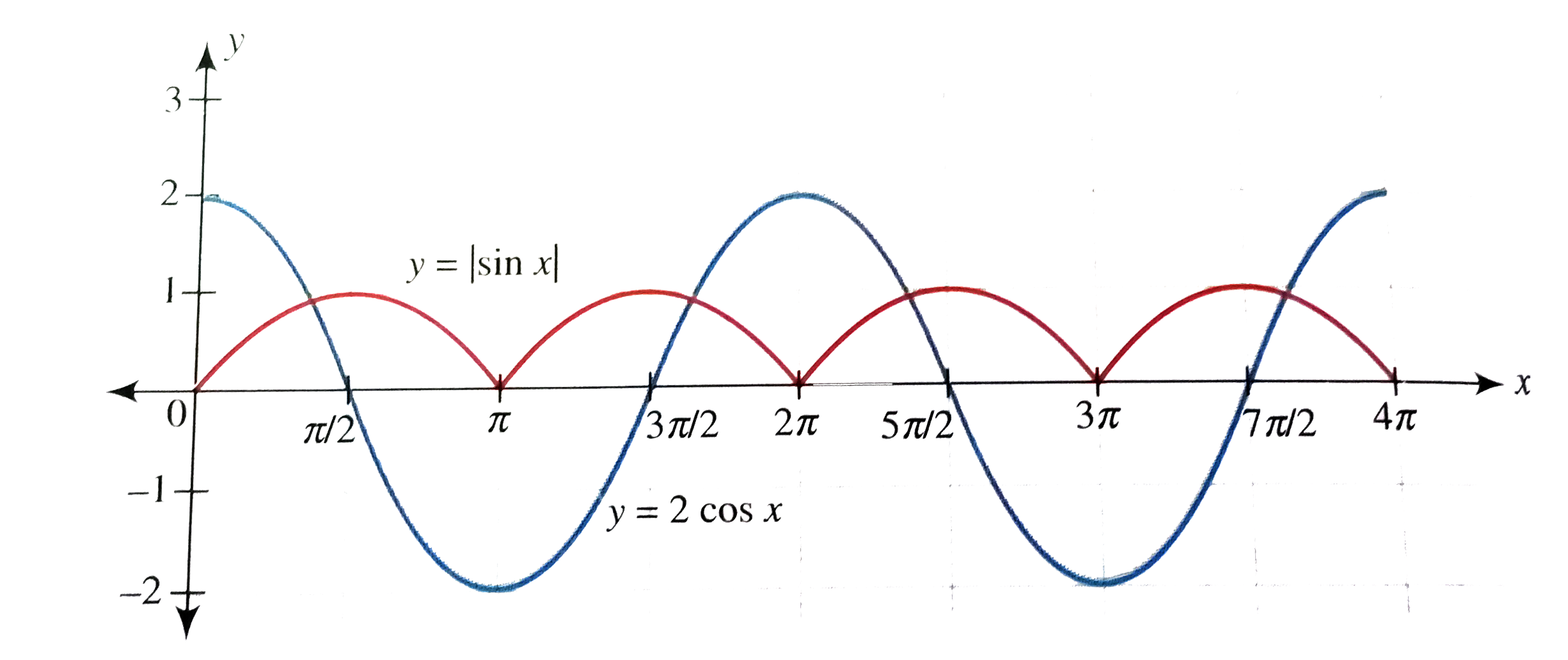
We find that the graphs intersect at four points. Hence the equation has four solutions.
Topper's Solved these Questions
Similar Questions
Draw the graph of y=tan−1x−cot−1x.
View SolutionDraw the graph of y=(x−1)(x2−x+1).
View SolutionIf x satifies |x−1|+|x−2|+|x−3|≥6, then (a)0≤x≤4 (b). x≤−2or≥4 (c). x≤0orx≥4 (d). None of these
View SolutionThe number of solutions of the equation |cosx−sinx|=2cosx∈[0,2π] is (A) 1 (B) 2 (C) 3 (D) 4
View SolutionIf 0≤x≤2π, then the number of solutions of 3(sinx+cosx)−2(sin3x+cos3x)=8 is
View SolutionThe number of solution of sinx+sin2x+sin3x=cosx+cos2x+cos3x,0≤x≤2π, is (a)7 (b)5 (c) 4 (d) 6
View SolutionThe number of real solutions of the equation √1+cos2x=√2sin−1(sinx),−π≤x≤π is (a) 0 (b) 1 (c) 2 (d) infinite
View SolutionThe number of solutions of 2cosx=|sinx|,0≤x≤4π, is (a) 0 (b) 2 (c) 4 (d) infinite
View SolutionIf x satifies |x−1|+|x−2|+|x−3|≥6, then (a)0≤x≤4 (b). x≤−2or≥4 (c). x≤0orx≥4 (d). None of these
View SolutionThe number of real solutions of the equation √1+cos2x=√2sin−1(sinx),−π≤x≤π is 0 (b) 1 (c) 2 (d) infinite
View SolutionThe number of solutions of 2cosx=|sinx|,0≤x≤4π, is (a) 0 (b) 2 (c) 4 (d) infinite
View SolutionThe number of real solutions of the equation √1+cos2x=√2sin−1(sinx),−π≤x≤π is (a) 0 (b) 1 (c) 2 (d) infinite
View SolutionThe number of solutions of the equation |cosx−sinx|=2cosx∈[0,2π] is (A) 1 (B) 2 (C) 3 (D) 4
View SolutionIf 0≤x≤2π, then the number of solutions of 3(sinx+cosx)−2(sin3x+cos3x)=8 is
View SolutionThe number of solution of sinx+sin2x+sin3x=cosx+cos2x+cos3x,0≤x≤2π, is (a)7 (b)5 (c) 4 (d) 6
View SolutionThe number of solutions of 2cosx=|sinx|,0≤x≤4π, is 0 (b) 2 (c) 4 (d) infinite
View Solution
