Area of the triangle formed by the line x+y=3 and the angle bisectors of the pairs of straight lines x2−y2+2y=1 is (a) 2 sq units (b) 4 sq units (c) 6 sq units (d) 8 sq unitsSolution in Bengali
2 sq . Units
4 sq . Units
6 sq. units
8 sq. units
The correct Answer is:1
x2−y2+2y=1orx=±(y−1)
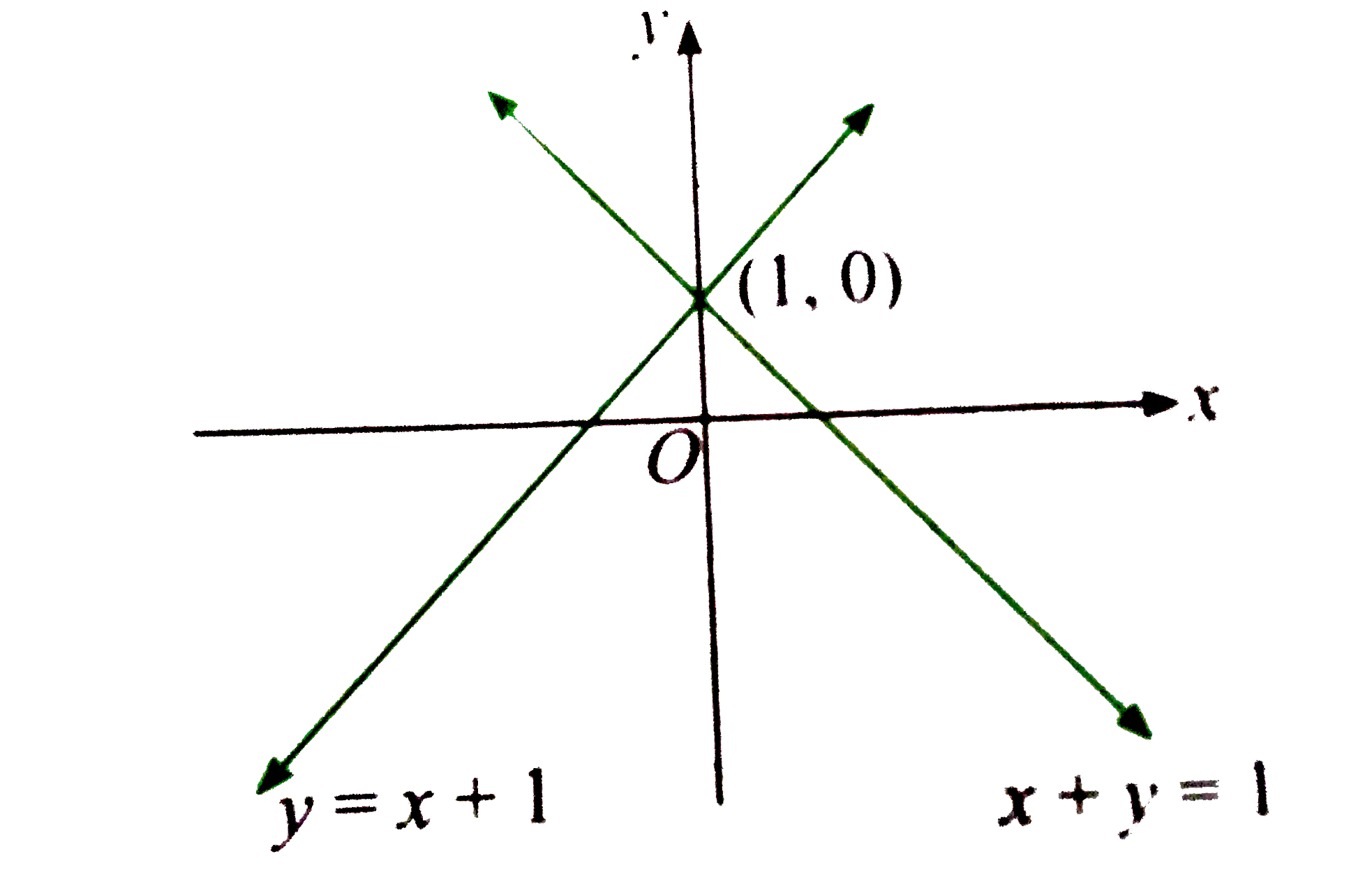
The bisectors of the above lines are x=0andy=1.
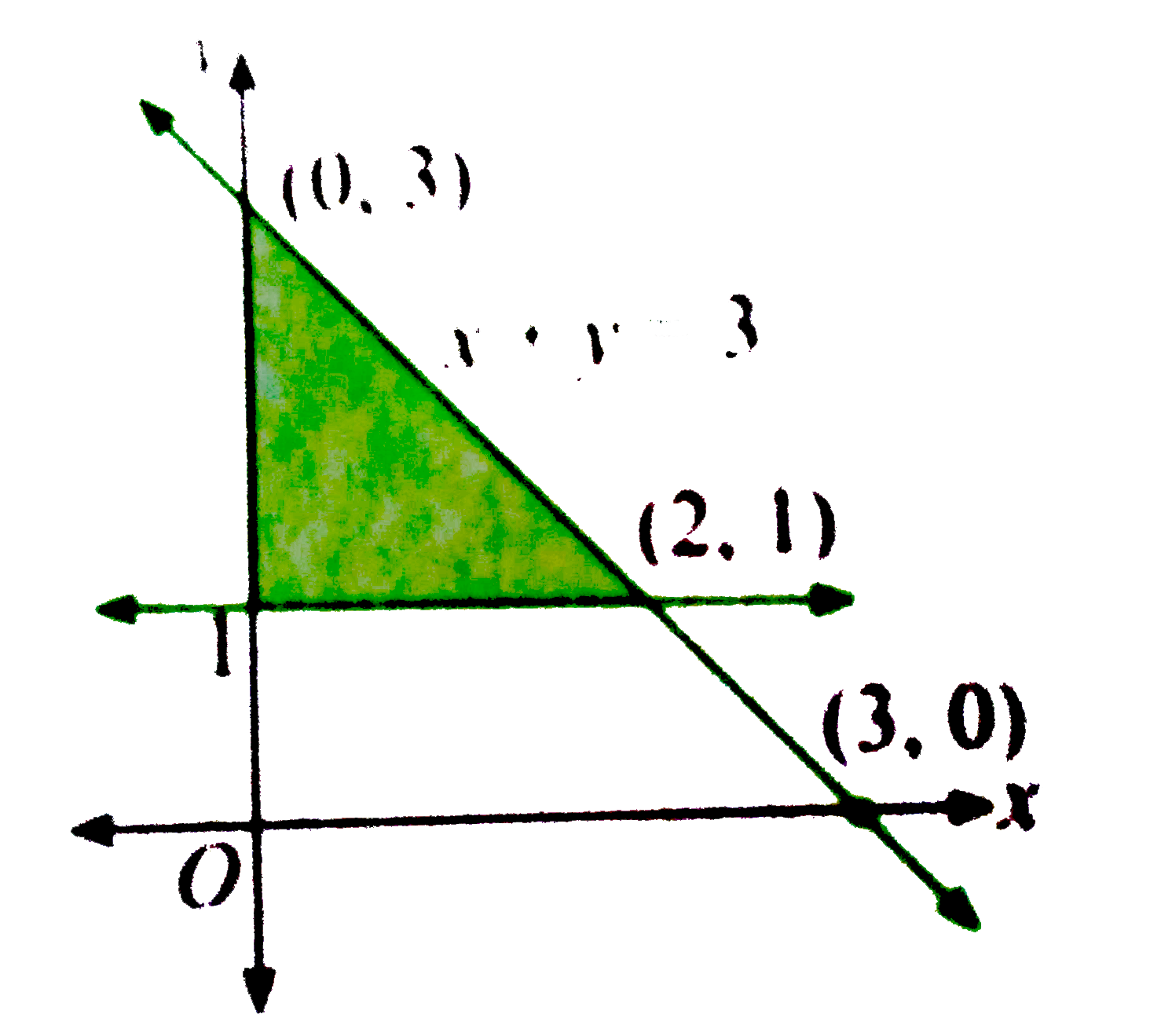
So , the area between x=0,y=1,andx+y=3 is the shaded region shown in the figure . The area is given by (1/2)×2×2=2 sq. units.
Topper's Solved these Questions
- PAIR OF STRAIGHT LINESBOOK - CENGAGE PUBLICATIONCHAPTER - PAIR OF STRAIGHT LINESEXERCISE - Multiple Correct Answer Type
9 Videos
- PAIR OF STRAIGHT LINESBOOK - CENGAGE PUBLICATIONCHAPTER - PAIR OF STRAIGHT LINESEXERCISE - Linked Comprehension Type
6 Videos
- PAIR OF STRAIGHT LINESBOOK - CENGAGE PUBLICATIONCHAPTER - PAIR OF STRAIGHT LINESEXERCISE - Exercise 3.2
7 Videos
- MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONSBOOK - CENGAGE PUBLICATIONCHAPTER - MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONSEXERCISE - Comprehension Type
6 Videos
- PARABOLABOOK - CENGAGE PUBLICATIONCHAPTER - PARABOLAEXERCISE - Matching Column Type
1 Videos
Similar Questions
The equation x3+x2y−xy2=y3 represents
View SolutionIf λx2−10xy+12y2+5x−16y−3=0, represents a pair of straight lines, then the value of λ is
View SolutionIf the slope of one line is double the slope of another line and the combined equation of the pair of lines is (x2a)+(2xyh)+(y2b)=0 , then find the ratio ab:h2.
View SolutionLet f:R→R,y=f(x),f(0)=0,f'(x)>0andf''(x)>0. Three point A(α,f(α)),B(β,f(β)),C(γ,f(γ))ony=f(x) such that 0<α<β<γ.
Which of the following is false ?
View SolutionAB is a chord of y2=4x such that normals at A and B intersect at C(9,6) and the tengent at A and B at point T, find (CT)2/13
View SolutionThe area bounded by the parabola y=(x+1)2 and y=(x−1)2 and the line y=14 is (A) 4 sq. units (B) 16 sq. units (C) 34 sq. units (D) 13 sq. units
View SolutionThe area of the region bounded by the curves y=|x−1| and y=3−|x| is (A) 6 sq. units (B) 2 sq. units (C) 3 sq. units (D) 4 sq. units
View SolutionThe area bounded by the curves y=logex and y=(logex)2 is (A) e−2 sq. units (B) 3−e sq. units (C) e sq. units (D) e−1 sq. units
View SolutionThe area bounded by the curves y=|x|−1andy=−|x|+1 is 1 sq. units (b) 2 sq. units 2√2 sq. units (d) 4 sq. units
View SolutionThe area bounded by the parabolas y=(x+1)2 and y=(x−1)2andy=(x−1)2 and the line y=14 is 4 sq. units (b) 1/6 sq. units 4/3 sq. units (d) 1/3 sq. units
View SolutionThe area enclosed by 2|x|+3|y|≤6 is (a)3 sq. units (b) 4 sq. units (c)12 sq. units (d) 24 sq. units
View SolutionArea of the triangle formed by the line x+y=3 and the angle bisectors of the pairs of straight lines x2−y2+2y=1 is (a) 2 sq units (b) 4 sq units (c) 6 sq units (d) 8 sq units
View SolutionThe area bounded by the curves y=|x|−1andy=−|x|+1 is 1 sq. units (b) 2 sq. units 2√2 sq. units (d) 4 sq. units
View SolutionThe area of the triangle formed by the line x=3, y=4 and x=y is (a)12sq.unit (b)1sq.unit (c)2sq.unit (d) None of these
View SolutionThe area of the triangle formed by the coordinate axes and the normal to the curve y=e2x+x2 at the point (0,1) is a)0 b)1 sq unit c)12sq unit d)2 sq unit
View SolutionThe area between the curve y=1−|x| and the x axis is equal to a)1 sq unit b)12 sq unit c)13 sq unit d)2 sq unit
View Solution
