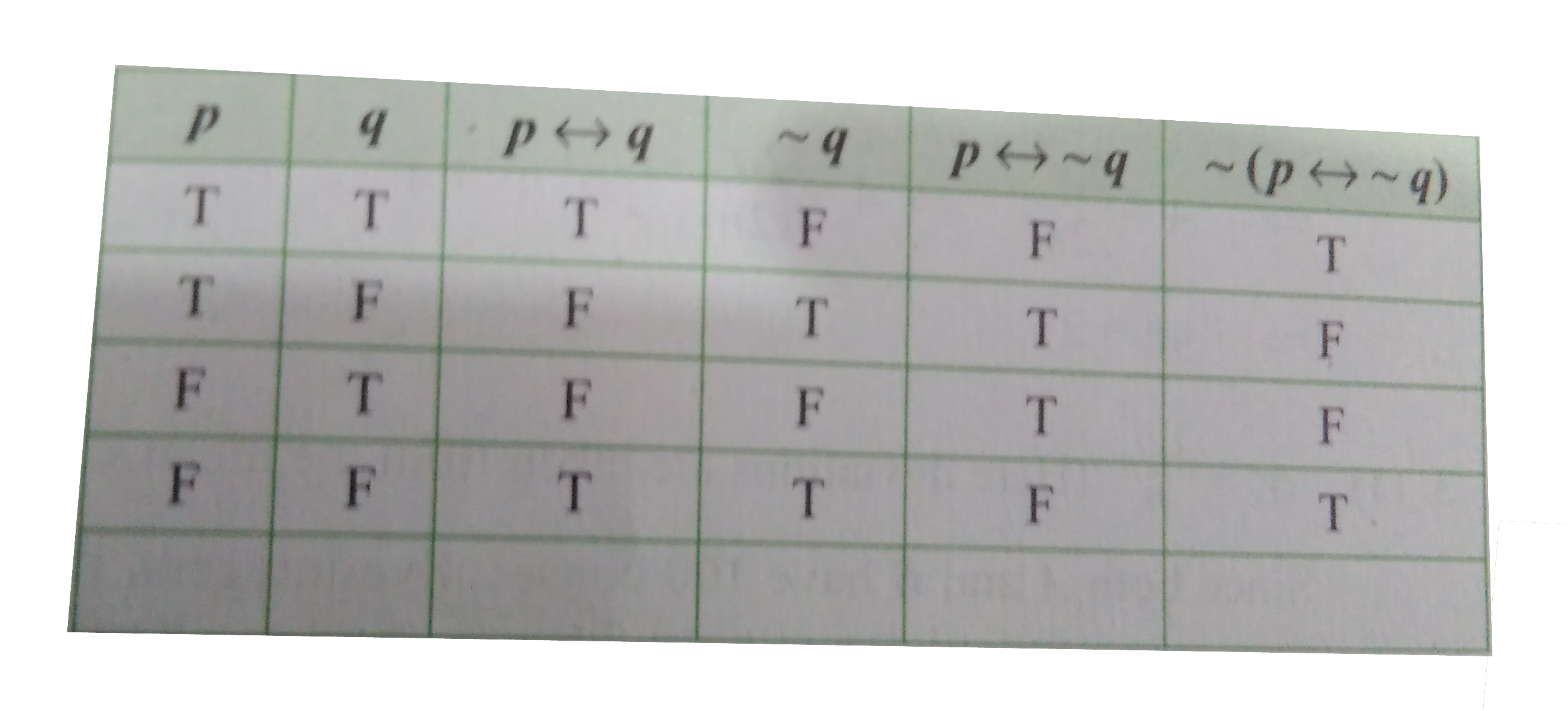Statements -1 : ~(p↔~q) is equivalent to p↔q
Statement-2: ~(p↔~q) is a tautology. Solution in Bengali
Statement-1 is true, statement 2 is true, statement 2 is a correct explanation for statement 1
Statement 1 is true, statement-2 is true, statement 2 is not a correct explanation for statement 1
Statement 1 is true , statement 2 is false,
statement 1 is false, statement 2 is true
The correct Answer is:C
Topper's Solved these Questions
- MATHMETICAL REASONINGBOOK - CENGAGE PUBLICATIONCHAPTER - MATHMETICAL REASONINGEXERCISE - Single correct answer type
38 Videos
- LOGARITHM AND ITS PROPERTIESBOOK - CENGAGE PUBLICATIONCHAPTER - LOGARITHM AND ITS PROPERTIESEXERCISE - JEE ADVANCED
1 Videos
- MATRICESBOOK - CENGAGE PUBLICATIONCHAPTER - MATRICESEXERCISE - All Questions
509 Videos
Similar Questions
Which of the following is not a statement.
View SolutionLet (x0,y0) be the solution of the following equations: (2x)1n2=(3y)1n3 31nx=21ny The x0 is 16 (b) 13 (c) 12 (d) 6
View SolutionIn which of the following type of matrix inverse does not exist always? a. idempotent b. orthogonal c. involuntary d. none of these
View SolutionThe equivalent statement of (p↔q) is-
View SolutionFind the truth values of
(a)(p↔~q)↔(p→p) (b)(p→q)∨~(p↔~q)
View SolutionConsider :
Statement I:
(p∧~q)∧(~p∧q) is a fallacy
Statement II: (p→q)↔(~q→~p) is a tautology
View SolutionStatement-1 : (p∧~q)∧(~p∧q) is a fallacy.
Statement -2: (p→q)↔(~q→~p) is a tautology .
View SolutionSTATEMENT-1 : ~(p⇔q)=~p⇔q=p⇔~q
and
STATEMENT-2 : (p⇔q)⇔r=p⇔(q⇔r)
View SolutionThe statement (~(p⇔q))∧p is equivalent to
View SolutionThe compound statement (p⇔q)∨(p⇔~q) is logically equivalent to
View SolutionStatement-1: ~(p↔~q) is equivalent to (p↔q).
Statement-2: ~(p↔~q) is a tautology.
View SolutionLet p and q be any two propositons
Statement 1 : (p→q)↔q∨~p is a tautology
Statement 2 : ~(~p∧q)∧(p∨q)↔p is fallacy
View Solutionकथन - 1 : ~ (p ↔ ~ q) और p ↔ q तुल्यमान (equivalent) हैं।
कथन -2: ~ (p↔ ~q) एक पुनरुक्ति (tautology) है ।
View SolutionFind the truth values of
(a)(p↔~q)↔(p→p) (b)(p→q)∨~(p↔~q)
View SolutionConsider :
Statement I:
(p∧~q)∧(~p∧q) is a fallacy
Statement II: (p→q)↔(~q→~p) is a tautology
View SolutionProve that the statement -~(p↔q)↔{(p∧~q)∨(~p∧q)} is a tautology.
View Solution