Question

Let A be a set containing elements. A subset P of the set A is chosen at random. The set A is reconstructed by replacing the elements of P, and another subset Q of A is chosen at random. The probability that $P\cap Q$ contains exactly $m(m<n)$ elements, is

Options

A. `(3^(n-m))/(4^(n))`
B. `(.^(n)C_(m).3^(m))/(4^(n))`
C. `(.^(n)C_(m).3^(n-m))/(4^(n))`
D. none of these

Answer

C

Explanation

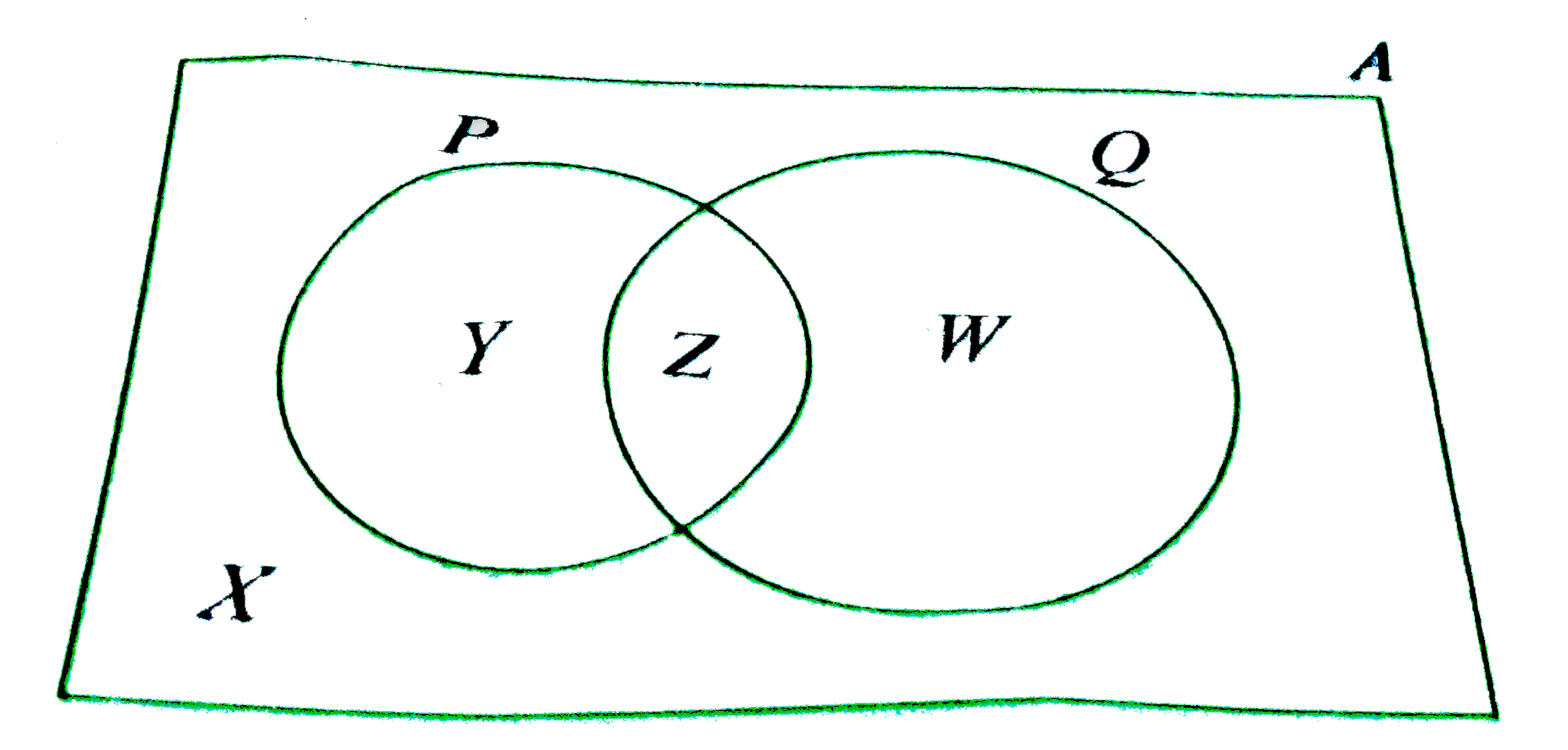
Sets P and Q are subsets of set A. Sets P and Q are dividing set A in four regions X, Y, Z and W.
`therefore` Total number of cases
= Number of ways in which n elements can be distributed in four regions = `4^(n)`
If set `(P nn Q)` has exactly m elements, we can select these m elements in `.^(n)C_(m)` ways. Remaining n - m elements can be distributed in the regions X, Y and W in `3^(n-m)` ways.
`therefore` Number of favourable ways = `.^(n)C_(m) xx 3^(n-m)`
`therefore` Required probability = `(.^(n)C_(m) xx 3^(n-m))/(4^(n))`