सरल आवर्ती गति करते किसी कण का विस्थापन y=A0+Asinωt+Bcosωt द्वारा निरूपित किया गया है तब इसके दोलन का आयाम होगा
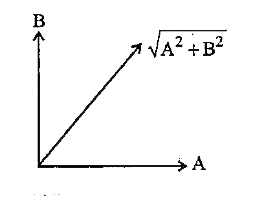
A0+√A2+B2
√A2+B2
√A20+(A+B)2
A+B
The correct Answer is:B
दिया गया सेमि
y=A0+sinωt+Bsinωt
अब मान लेते है =y
y−A0=Asinωt+Bsinωt
y=Asinωt+Bcosωt
=√A2+B2sin(ωt+ϕ)
यहाँ SHM है
यहाँ cosϕ=A√A2+B2
sinϕ=B√A2+B2
अतः परिणामी अयं
=√A2+B2
Topper's Solved these Questions
Similar Questions
किसी स्वरित्र द्विभुज का उपयोग किसी ऐसी काँच की नलिका में अन्नुकद उत्पन्न करने के लिया गया है, जिसमे वायु स्तम्भ की लम्बाई को परिवर्ती पिस्टन द्वारा समायोजित किया जा सकता है। 27∘C कक्ष ताप पर स्तम्भ की लम्बाई 20 सेमी और 73 सेमी होने पर दो क्रमागत अनुनाद उत्पन्न होते है। यदि स्वरित्र द्विभुज की आवृत्ति 320 हर्ट्स है, तो वायु में ध्वनि का 27∘C पर वेग है:
View Solutionदो गुटकों A और B के द्रव्यमान, क्रमश: 3m तथा m हैं। ये आपस में एक द्रव्यमानहीन, अवितान्य डोरी से जुड़े हैं। इस पूरे निकाय को, आरेख में दर्शाए गए अनुसार एक द्रव्यमानरहित स्प्रिंग (कमानी) द्वारा लटकाया गया है। डोरी को काट देने के तुरन्त पश्चात् A और B के त्वरण के परिमाण होंगे क्रमशः
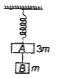
View SolutionEquations y=2 A cos^2 omega t and y = A ( sin omega t + sqrt3 cos omega t) represent the motion of two particles.
View Solutionगति का वर्णन || निर्देश तंत्र || सरल रेखीय गति || एकसमान गति और असमान गति || दूरी || विस्थापन ||
View SolutionIf f1(t)=Asinωtandf2(t)=Bcosωt, then say whether f(t)=Asinωt+Bcosωt is also periodic.
View Solutionगति का वर्णन || निर्देश तंत्र || सरल रेखीय गति || दूरी || विस्थापन ||
View Solutionदोलन| सरल आवर्त गति का विस्थापन समीकरण
View Solutionदोलन|सरल आवर्त गति #!# सरल आवर्त गति का वेग समीकरण
View Solutionदोलन|सरल आवर्त गति #!#सरल आवर्त गति में त्वरण तथा आवर्तकाल का व्यंजक
View Solutionदोलन |सरल आवर्त गति #!#कोणीय सरल आवर्त गति #!#सरल लोलक
View SolutionOut of the following functions representing motion of a particle which represent SHM? (a) y= sin omega t- cos omega t (b) y= sin^(2) omega t (c ) y= 5cos ((3pi)/(4)-3 omega t) (d) y= 1+ omega t+ omega^(2) t^(2)
View Solutionदोलन और आवर्ती गति
View Solutionआवर्ती गति |दोलन गति या कंपन गति
View Solutionस्तम्भ- I की प्रत्येक स्थिति में x-दिशा में गति करते हुए कण का समय t के पदों में x-निर्दर्शक दिया है। (ω धनात्मक नियतांक है) स्तम्भ-I में दी गई गति के समीकरण को स्तम्भ- II में गति के प्रकार से सुमेलित करिये-
स्तम्भ-I स्तम्भ-II (A)sinωt−cosωt(p)सरल आवर्त गति (SHM)(B)sin3ωt(q) आवर्त (periodic) गति(C)sinωt+sin3ωt+sin5ωt(r) आवृति गति पर सरल आवर्त गति नहीं (D)exp(−ω2t2)(s)कोई आवर्त गति नहीं
View Solutionx=Acosωt+Bsinωt, the amplitude of this wire is:
View Solution
