Question

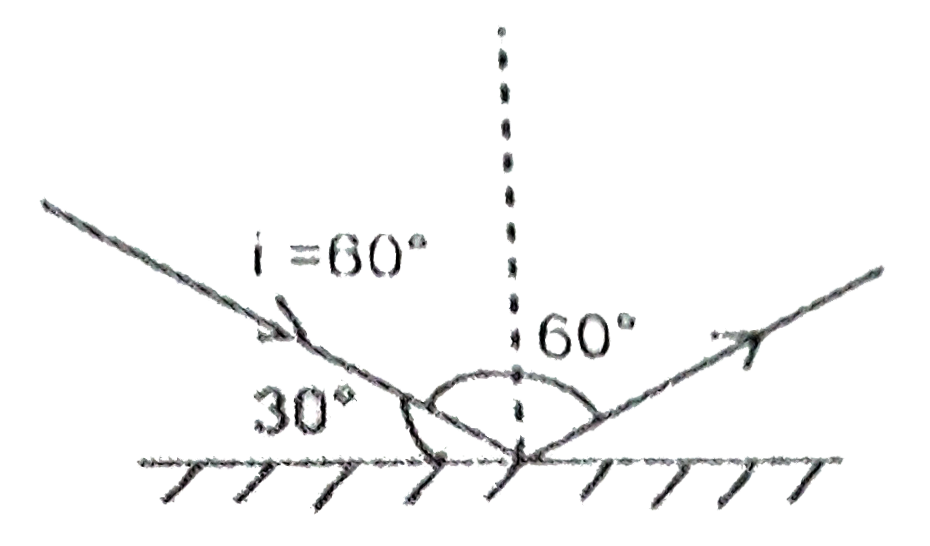
If a ray of light falling on a mirror makes an angle of ${\displaystyle {60}^{\circ }}$ with the mirror, then the angle between the incident and reflected rays will be ______.

Options

A. `30^@`
B. `60^@`
C. `90^@`
D. `120^@`

Answer

B

Explanation

To solve the problem, we need to determine the angle between the incident ray and the reflected ray when a ray of light falls on a mirror at an angle of $${60}^{\circ }$$ with respect to the mirror surface.

1. Understanding the Setup:
- We have a mirror, and a ray of light is incident on it. The angle given (60 degrees) is with respect to the mirror surface.

2. Identifying the Normal:
- The normal is an imaginary line that is perpendicular to the surface of the mirror at the point of incidence. Since the mirror is flat, the normal makes a \(90^\circ\) angle with the mirror surface.

3. Calculating the Angle with the Normal:
- If the angle between the incident ray and the mirror surface is \(60^\circ\), then the angle between the incident ray and the normal can be calculated as:
\( \text{Angle with normal} = 90^\circ - 60^\circ = 30^\circ \)
- Let’s denote this angle as \(\alpha\).

4. Applying the Law of Reflection:
- According to the law of reflection, the angle of incidence (\(\alpha\)) is equal to the angle of reflection (\(\beta\)). Therefore:
\( \beta = \alpha = 30^\circ \)

5. Finding the Angle Between Incident and Reflected Rays:
- The angle between the incident ray and the reflected ray is the sum of the angles \(\alpha\) and \(\beta\):
\( \text{Angle between incident and reflected rays} = \alpha + \beta = 30^\circ + 30^\circ = 60^\circ \)

6. Conclusion:
- Therefore, the angle between the incident and reflected rays is \(60^\circ\).

Final Answer:
The angle between the incident and reflected rays will be \(60^\circ\).

---