If the lengths of two poles P1 and P2 are 26.79 m and 29.34m, respectively, then how much longer is P2 than P1?
2.45m
2.35m
2.55m
2.65m
The correct Answer is:C
To find out how much longer pole P2 is than pole P1, we can follow these steps:
Step 1: Identify the lengths of the poles
- Let the length of pole P1 (L1) be 26.79 meters.
- Let the length of pole P2 (L2) be 29.34 meters.
Step 2: Set up the equation to find the difference
To find out how much longer P2 is than P1, we need to subtract the length of P1 from the length of P2. The equation will be:
\( \text{Difference} = L2 - L1 \)
Step 3: Substitute the values into the equation
Now, substitute the values of L1 and L2 into the equation:
\( \text{Difference} = 29.34 - 26.79 \)
Step 4: Perform the subtraction
Now, let's perform the subtraction:
- Align the numbers for easier calculation:
29.34−26.79−−−−−−−
- Start from the rightmost digit:
- 4 - 9: Since 4 is less than 9, we need to borrow 1 from the next column. So, 14 - 9 = 5.
- Next column: 2 (after borrowing it becomes 1) - 7: Again, we need to borrow. So, 12 - 7 = 5.
- Next column: 2 (after borrowing it becomes 1) - 6: We need to borrow again. So, 12 - 6 = 6.
- Finally, 2 - 2 = 0.
So, the result of the subtraction is:
\( 29.34 - 26.79 = 2.55 \)
Step 5: State the final answer
Thus, the length of pole P2 is 2.55 meters longer than pole P1.
Final Answer:
P2 is 2.55 meters longer than P1.
---
- Let the length of pole P1 (L1) be 26.79 meters.
- Let the length of pole P2 (L2) be 29.34 meters.
To find out how much longer P2 is than P1, we need to subtract the length of P1 from the length of P2. The equation will be:
\( \text{Difference} = L2 - L1 \)
Now, substitute the values of L1 and L2 into the equation:
\( \text{Difference} = 29.34 - 26.79 \)
Now, let's perform the subtraction:
- Align the numbers for easier calculation:
29.34−26.79−−−−−−−
- Start from the rightmost digit:
- 4 - 9: Since 4 is less than 9, we need to borrow 1 from the next column. So, 14 - 9 = 5.
- Next column: 2 (after borrowing it becomes 1) - 7: Again, we need to borrow. So, 12 - 7 = 5.
- Next column: 2 (after borrowing it becomes 1) - 6: We need to borrow again. So, 12 - 6 = 6.
- Finally, 2 - 2 = 0.
\( 29.34 - 26.79 = 2.55 \)
Thus, the length of pole P2 is 2.55 meters longer than pole P1.
P2 is 2.55 meters longer than P1.
Topper's Solved these Questions
- NUMBER SYSTEMBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - NUMBER SYSTEMEXERCISE - CONCEPT APPLICATION (LEVEL 3)
17 Videos
- NUMBER SYSTEMBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - NUMBER SYSTEMEXERCISE - ASSESSMENT TESTS
24 Videos
- NUMBER SYSTEMBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - NUMBER SYSTEMEXERCISE - CONCEPT APPLICATION (LEVEL 1)
19 Videos
- MOCK TESTBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - MOCK TESTEXERCISE - QUESTIONS
25 Videos
- RATIO AND ITS APPLICATIONSBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - RATIO AND ITS APPLICATIONSEXERCISE - ASSESSMENT TESTS (TEST 2)
12 Videos
Similar Questions
Two pipes P1 and P2 are closed and open respectively. P1 has a length of 0.3m. Find the length of P2, if third harmonic of P1 is same as first harmonic of P2.
View SolutionP1andP2 are planes passing through origin, L1andL2 are two lines on P1andP2 respectivelym such that their intersection is the origin. Show that there exist points, A, B and C , whose perpmutation, A, B' and C' respectively, can be chosen such that (i) A is on L1'BandP1 put not on L1andC not on P1 , (ii) A is on L2,B'onP2 but not on L2andC' not on P2 .
View Solution
Knowledge Check
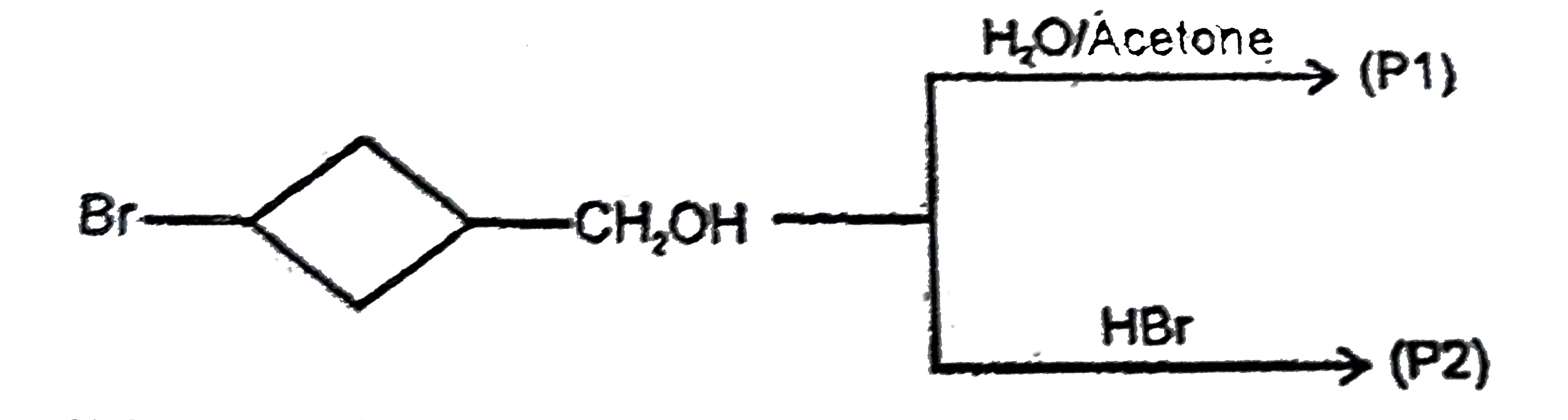
P1 and P2 are respectively :A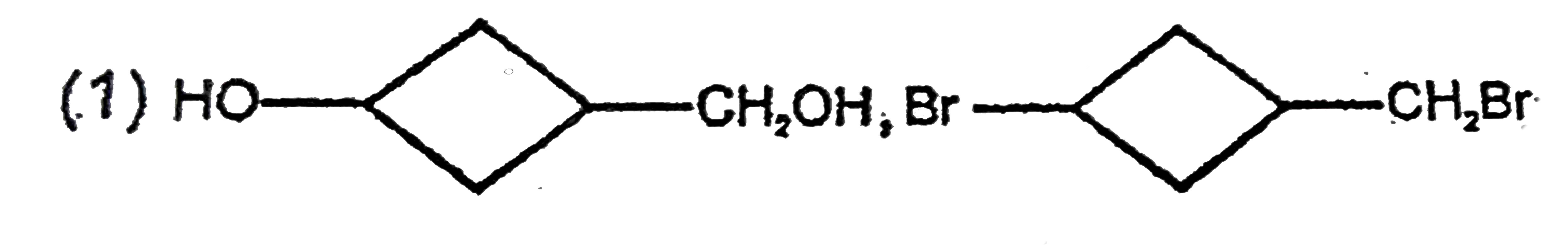 B
B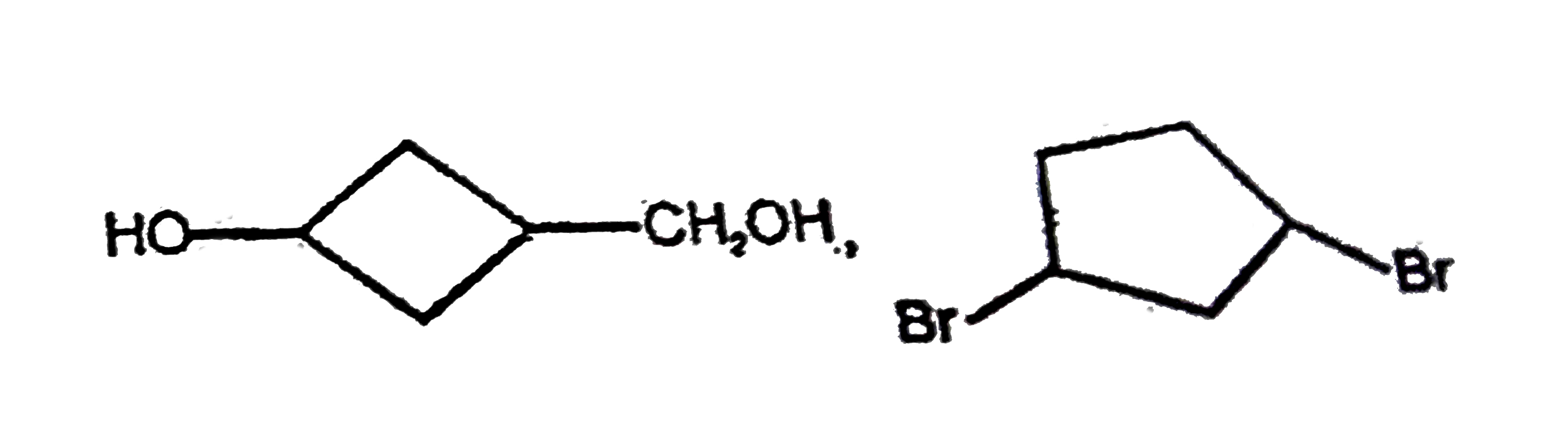 C
C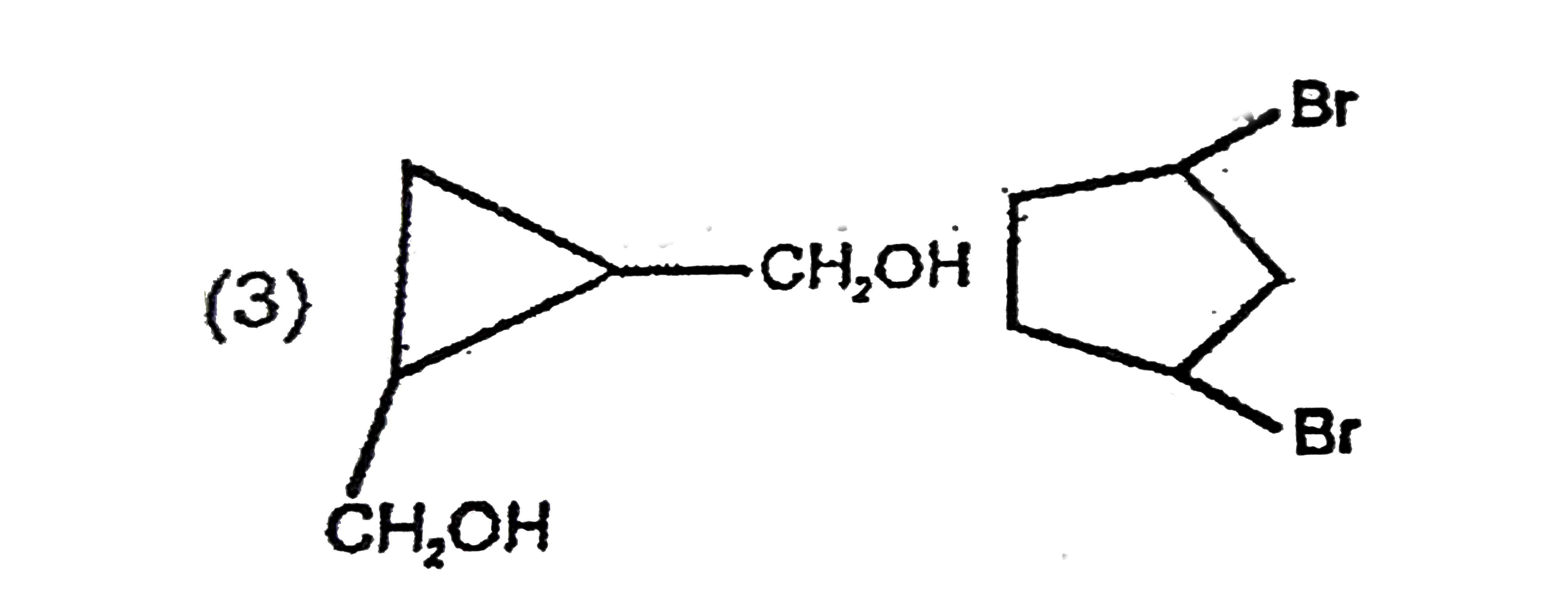 D
D
The radius of the cross-sections of pipes P1 and P2 are 7 m and 14 m respectively. Water flows through P1 at a constant rate of 10 m/s and it can alone fill a tank in 2 hours. If P1 is used as the inlet pipe and P2 as the outlet pipe then together they fill the tank in 4 hours. What is the rate of water flow (in m/s) through P2?
Aa)1.00Bb)1.25Cc)1.50Dd)2.000.1 M NaCl and 0.1MCH3COOH are kept in separate containers. If their osmotic pressures are P1 and P2 respectively then what is the correct statement ?
AP1>P2BP1=P2CP1<P2DP1=P2=0 atm
P1andP2 are planes passing through origin, L1andL2 are two lines on P1andP2 respectivelym such that their intersection is the origin. Show that there exist points, A, B and C , whose perpmutation, A, B' and C' respectively, can be chosen such that (i) A is on L1'BandP1 put not on L1andC not on P1 , (ii) A is on L2,B'onP2 but not on L2andC' not on P2 .
View SolutionIn the Young's double slit experiment, the intensities at two points P1 and P2 on the screen are respectively I1 and I2 If P1 is located at the centre of a bright fringe and P2 is located at a distance equal to a quarter of fringe width from P1 then I1I2 is
View SolutionThree identical conducting plates P1,P2 and P3 are kept at a distance d from each other. If q,-q,2q are the charges in P1,P2 and P3 respectively, the electric field between P1 and P2 is (where A is area of plate)
View SolutionTwo pipes P1 and P2 can fill a tank in 8 h and 5 h, respectively. They are opened together, after an hour, pipe P2 is closed, in how many more hours will the tank be filled?
View SolutionIf two liquids of same masses but densities p1 and p2, respectively are mixed, then the density of mixture is given by
View Solution
